Multilevel-methods with high order in time and space for the numerical simulation of incompressible flows
High-order methods achieve a higher convergence rate than established numerical methods and, hence, offer a large potential for the simultaneous optimization of the speed and accuracy of flow simulations. To exploit this advantage, the orders in space and time must be attuned to each other. However, while powerful high-order methods exist for spatial discretization, practical time integration schemes reach only order 2 up to 4 for incompressible flows. As a consequence, the time discretization becomes the limiting factor. It constrains the overall order of the method to values that are already achieved with conventional finite element methods and finite volume methods. The project intends to break through this barrier. This will be accomplished by developing semi-implicit multi-level methods which enable the numerical simulation of incompressible flows with arbitrary order in space and time.
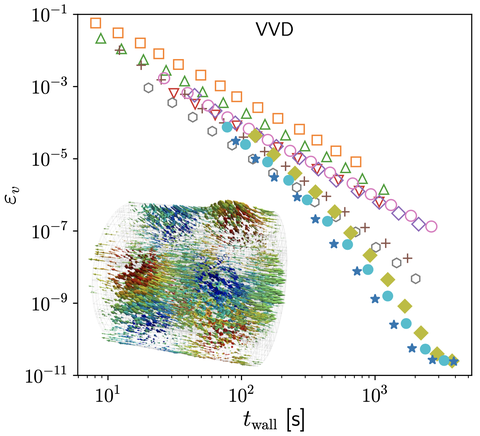
Efficiency of high-order time integration methods
The main idea consists in combining the spectral deferred correction (SDC) method with tailored splitting schemes. The ability to overcome the order barrier of conventional methods with this approach was demonstrated in preliminary studies at the example of the Stokes equations. The present project will extend this method substantially and develop an SDC for incompressible Navier- Stokes problems including a variable viscosity. The principal milestones are: 1) generation and analysis of new SDC methods with high stability and low iteration count, 2) achievement of an order-independent convergence rate by means of multilevel SDC, 3) minimization of the cost for solving the discrete equations via space-time multigrid, 4) generalization to varying coefficients including the extension to large-eddy simulation.
For spatial discretization, the project focuses on nodal discontinuous Galerkin methods. With this approach orders from 4 to 32 are targeted – in space as well as in time.
As a result, the project provides the first semi-implicit time integration method of arbitrarily high order for incompressible Navier-Stokes problems with variable viscosity. Combined with the highly efficient multi-level methods for solving the discrete equations, it opens an attractive perspective for the application of high-order methods in fluid mechanics. The generalization of these techniques in possible follow-up projects promises an approach to far more complex problems, such as configurations with curved boundaries or multi-phase flows.
| Cooperation | Michael Minion, Berkley Lab |
| Funding | DFG under grant STI 157/8-1 |
| Contact | M. Sc. Martina Grotteschi PD Dr. Jörg Stiller |
