Multilevel-Methoden hoher Ordnung in Zeit und Raum für die numerische Simulation inkompressibler Strömungen
Numerische Methoden hoher Ordnung erzielen im Vergleich zu etablierten Verfahren eine höhere Konvergenzrate und bieten dadurch ein großes Potenzial zur gleichzeitigen Optimierung der Geschwindigkeit und Präzision von Strömungssimulationen. Um die Stärken solcher Methoden voll auszuspielen, muss die Genauigkeit in Ort und Zeit aufeinander abgestimmt werden. Während für die Ortsdiskretisierung leistungsfähige Methoden bereitstehen, erreichen praktikable Zeitintegrationsmethoden für inkompressible Strömungen aber nur Ordnung 2 bis 4. Dadurch wird die Zeitdiskretisierung zum limitierenden Faktor. Sie schränkt die Ordnung des Gesamtverfahrens auf Werte ein, die bereits mit konventionellen Finite-Elemente-Methoden und Finite-Volumen-Methoden erreicht werden. Diese Schranke will das Projekt durchbrechen. Dazu werden semi-implizite Multilevel-Methoden entwickelt, welche die numerische Simulation inkompressibler Strömungen mit beliebig hoher Ordnung in Raum und Zeit ermöglichen.
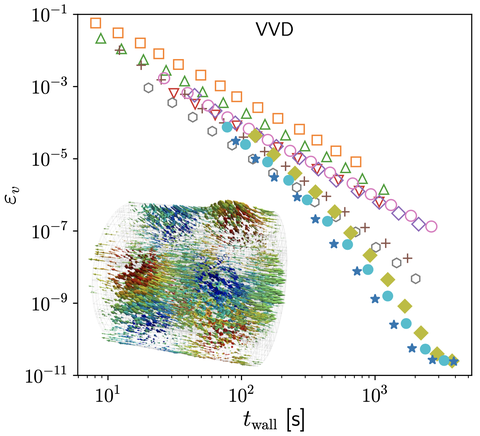
Effizienz von Zeitintegrationsmethoden
Die wesentliche Idee besteht in der Verschmelzung der spektralen verzögerten Korrektur (Spectral Deferred Correction – SDC) mit maßgeschneiderten Splitting-Methoden. Dass es möglich ist, mit diesem Ansatz die Ordnungsbarriere konventioneller Verfahren zu überwinden, wurde in Vorstudien am Beispiel der Stokes- Gleichung demonstriert. Im vorliegenden Projekt wird diese Methode substanziell erweitert und eine SDC für inkompressible Navier-Stokes-Probleme mit variabler Viskosität entwickelt. Wesentliche Meilensteine sind: 1) Ableitung und Analyse neuer SDC-Methoden mit hoher Stabilität und geringer Iterationszahl, 2) Erreichen einer von der Ordnung unabhängigen Konvergenzrate durch Multilevel-SDC, 3) Minimierung der Kosten für die Lösung der diskreten Gleichungen durch Raum-Zeit- Mehrgitterverfahren, 4) Verallgemeinerung auf variable Koeffizienten und Erschließung neuer Anwendungen inklusive Large-Eddy-Simulationen.
Bei der Ortsdiskretisierung konzentriert sich das Projekt auf nodale diskontinuierliche Galerkin- Methoden. Mit diesem Ansatz werden Ordnungen von 4 bis 32 anvisiert – sowohl im Raum als auch in der Zeit.
Im Ergebnis liefert das Projekt das erste semi-implizite Zeitintegrationsverfahren beliebig hoher Ordnung für inkompressible Navier-Stokes-Probleme mit variabler Viskosität. In Verbindung mit den hier entwickelten hoch effizienten Multilevel-Methoden für die Lösung der diskreten Gleichungen öffnet es attraktive Perspektiven für die Anwendung von Methoden hoher Ordnung in der Strömungsmechanik. Die Verallgemeinerung dieser Techniken in möglichen Folgeprojekten verspricht einen Zugang zu weitaus komplexeren Problemen, wie Konfigurationen mit gekrümmten Randflächen oder Mehrphasenströmungen.
| Kooperation |
Michael Minion, Berkley Lab |
| Finanzierung | DFG, Förderkenzeichen STI 157/8-1 |
| Kontakt |
