Teilprojekt B3

Numerische Untersuchungen zum Tragmechanismus von Filamentgarnen in einer Betonmatrix

Leitung

Prof. Dr.-Ing. habil. Ulrich Häußler-Combe
Institut für Massivbau

Mitarbeiter

Dr.-Ing. Jens Hartig
Dr.-Ing. Patrick Pröchtel (ehemaliger Mitarbeiter)

Ziele

Der Verbundwerkstoff textilbewehrter Beton stellt ein hochgradig heterogenes Gebilde sowohl in Bezug auf die Matrix als auch die Bewehrung dar. Bisherige Modellierungsansätze auf der Makro- und Mesoebene, die von weitgehend homogenen Materialien ausgehen, können zwar grundsätzlich das globale Tragverhalten abbilden, sind aber nicht geeignet, weitergehende Erkenntnisse über das Trag- und Versagenshalten, das seinen Ursprung auf der mikroskopischen Skale hat und experimentell nicht oder nur schwer zu erfassen ist, zu erbringen. Bestehende mikroskopische Modelle des textilbewehrten Betons beschränken sich auf die Betrachtung des Tragverhaltens homogener Garne und des Tragverhaltens des Verbundwerkstoffes an einem einzelnen Matrixriss. Im Hinblick auf das Tragverhalten von Textilbetonbauteilen mit vielfacher Rissbildung wird ein Forschungsbedarf deutlich.
Das Arbeitsprogramm der 1. Projektphase (3. Förderperiode des SFB528) beinhaltete die Definition eines mechanischen Modells unter Einbeziehung der als wesentlich erachteten Tragmechanismen und Systemparameter sowie der Entwicklung eines entsprechenden numerischen Modells. Zur Validierung des Modells sollten entsprechend den verfügbaren Versuchsdaten zu Filamentauszugsversuchen, unterbewehrten Zugversuchen und Zugversuchen mit mehrfacher Matrixrissbildung verschiedene Modellkonfigurationen verwendet werden. Darauf aufbauend sollten Parameterstudien durchgeführt werden, die zu einem vertieften Verständnis der Verbundmechanismen und den daraus resultierenden Trag- und Versagensmechanismen führen sollen. Dies sollte die mikromechanische Grundlage für die Modellierung auf der Meso- und Makroebene bilden. Zudem sollten Empfehlungen zur Effizienzsteigerung des Textilbetons aus beton- und textiltechnologischer Sicht gegeben werden.
Für das angestrebte Modell in der Mikroebene waren zunächst diejenigen Material- und Systemparameter zu bestimmen, die einen wesentlichen Einfluss auf das Tragverhalten haben. Dies sind z.B. die begrenzten Zugfestigkeiten sowohl der Bewehrung als auch der Matrix aus Feinbeton. In erster Näherung wurden die Heterogenität der Matrix und zunächst auch die Zugentfestigung der Matrix aufgrund der geringen Zuschlaggröße vernachlässigt. Im Gegensatz dazu wurde eine realitätsnahe Abbildung der Garnbewehrung in ihrer Zusammensetzung aus einer Vielzahl von Filamenten, auch aufgrund komplexer Verbundverhältnisse im Garn, als notwendig eingeschätzt. Der Verbund innerhalb eines Garnes kann zunächst in eine Zone adhäsiven Verbundes im Außenbereich des Garnes mit Matrixkontakt und eine Zone im Inneren des Garnes unterschieden werden, in der nur geringe Kräfte über Adhäsion im unmittelbaren Kontakt der Filamente untereinander übertragen werden können und somit von einem frühzeitigen Übergang zur Reibung ausgegangen wird. Daher ist ein erster sinnvoller Modellierungsansatz mit der Unterteilung der Garne in Rand- und Kernbereiche gegeben.
Aufbauend auf den Ergebnissen und Erkenntnissen der 1. Projektphase, die noch gewisse Defizite des bis dahin entwickelten Modells aufzeigten, wird für die 2. Projektphase (4. Förderperiode des SFB528) die Erweiterung des Modells als notwendig angesehen. Dies soll die Einbeziehung der Zugentfestigung der Matrix, der Welligkeit der Bewehrung und räumlich streuender Materialeigenschaften beinhalten. Anhand des so verbesserten Modells sollen mit geeigneten Verfahren Erkenntnisse und Empfehlungen zur Verbesserung und Optimierung des Verbundwerkstoffs erbracht werden. Darüber hinaus ist die Betrachtung bemessungsrelevanter Fragestellungen wie z.B. der Interaktion von Stahl- und Textilbeton und des Verhaltens von Textilbeton unter Zwangbeanspruchungen vorgesehen.

Ergebnisse

Modell

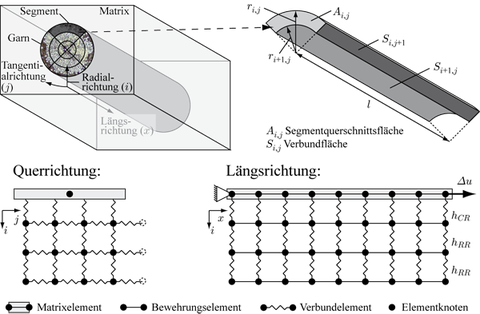
Die Grundlage des mechanischen Modells bildet das sogenannte Segmentmodell, vgl. Abb. 1, aus dem nach einer Diskretisierung mit der Finite Elemente Methode auch das numerische Modell abgeleitet wird. Dabei wird die Bewehrung in Segmente mit jeweils homogenem Verhalten unterteilt (Abb. 1, oben links) und schematisch in einem Gitter (Abb. 1, unten links) angeordnet. Das Verhalten der Matrix wird ebenfalls als homogen über den Querschnitt senkrecht zur Belastungsrichtung angenommen. Das Verhalten der Bewehrungssegmente und der Matrix wird durch Stabelemente approximiert, die als Eigenschaften einaxiale Materialgesetze unter Vernachlässigung von Querdehnungseffekten sowie eine Querschnittsfläche besitzen. Die Querschnittsfläche der Matrixstabelemente entspricht der Querschnittsfläche des Probekörpers während für die Bewehrungsstabelemente die Querschnittsfläche mit dem Segementierungsansatz bestimmt wird. In der Längsrichtung wird eine Vielzahl von Stabelementen in Reihe geschaltet (Abb. 1, unten rechts), um zum einen das multiple Rissverhalten der Matrix und der Bewehrung und zum anderen das Verbundverhalten zwischen den einzelnen Segmenten realitätsnah abbilden zu können.

Abb. 1: Geometrisches Modell und Segmentdiskretisierung

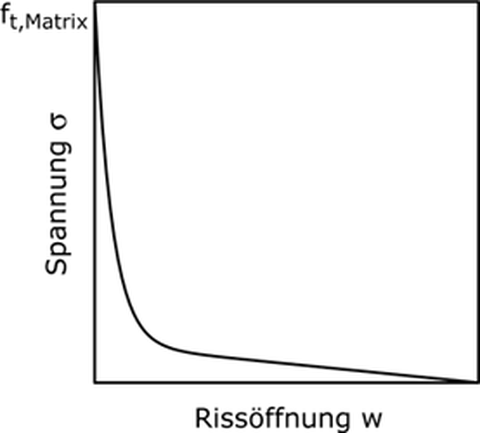
Für die Matrix wird linear-elastisches Verhalten entsprechend dem Elastizitätsmodul bis zum Erreichen der Zugfestigkeit angenommen. Nach Überschreiten der Zugfestigkeit kann in erster Näherung sprödes Versagen angenommen werden. Realitäsnäher ist jedoch dich Berücksichtigung der Zugentfestigung, welches mit einer Spannungs-Rissöffnungsbeziehung modelliert wird (Abb. 2a). Durch eine Regularisierung anhand des Riss-Band-Ansatzes wird eine entsprechende Spannungs-Dehnungsbeziehung für die Zugentfestigung erhalten.
Für die Bewehrung kann ebenfalls näherungsweise linear-elastisches Materialverhalten bis zum Erreichend der Zugfestigkeit angenommen werden. In Experimenten ist jedoch häufig eine verzögerte Aktivierung der Bewehrung aufgrund der vorhandenen Bewehrungswelligkeit zu beobachten. Dieser geometrische Effekt auf kleiner Skale wird im Materialgesetz durch einen allmählichen Übergang zum linearen Verlauf der gestreckten Bewehrung berücksichtigt (Abb. 2b).

Abb. 2: Materialgesetze für Matrix und Bewehrung: Entfestigungsgesetz für die Matrix (links),
Materialgesetz mit verzögerter Aktivierung für die Bewehrung (rechts)

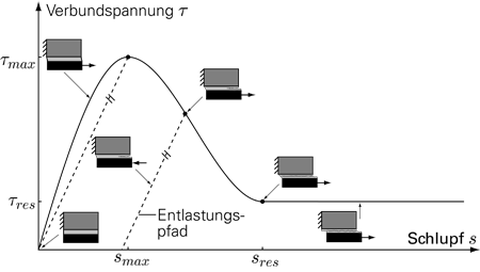
Die Stabelementketten werden an den Elementknoten über Verbundelemente miteinander gekoppelt. Die Geometrieeigenschaften eines Verbundelementes werden durch eine Verbundfläche beschrieben, die aus dem Segmentmodell abgeleitet wird (Abb. 1, oben rechts). Um die sich beim Auszug von Fasern reduzierende Verbundfläche mit einzubeziehen können, kann im Modell die Verbundfläche in Abhängigkeit der Lage des Verbundelements zu gerissenen Matrixelementen bestimmt werden. Die Verbundcharakteristiken werden in Form von Verbundspannungs-Schlupfbeziehungen (Abb. 3) als Materialgesetz den Verbundelementen zugewiesen. Die Eingangsgröße ist der Schlupf s, der sich aus der Relativverschiebung der beiden Knoten des Verbundelementes ergibt. Aus diesem lässt sich die Verbundspannung τ des entsprechenden Elementes berechnen. Der Verlauf des Verbundgesetzes wird über Stützstellen in Form von Wertepaaren (s, τ) definiert, zwischen denen interpoliert wird. Dabei wird das sogenannte "Piecewise Cubic Hermite Interpolating Polynomial" (PCHIP) genutzt. Dieses Verfahren verwendet kubische Polynome, welche Monotonie und Stetigkeit in ihren ersten Ableitungen zwischen aufeinanderfolgenden Abschnitten aufweisen. Dies reduziert numerische Probleme während der Berechnungen an den Übergängen der Abschnitte des Verbundgesetzes. Ein wichtiger Aspekt der Verbundmodellierung ist das Verhalten bei Entlastung. Im Verbundgesetz ist der vom Belastungspfad abweichende Entlastungspfad unter Annahme inelastischer Deformationen berücksichtigt (Abb. 2).

Abb. 3: Verbundspannungs-Schlupfgesetz

Zur Modellierung räumlich streuender Materialeigenschaften wird das Konzept der Zufallsfelder verwendet, wofür ein Ansatz basierend auf der Karhunen-Loève-Transformation zum Einsatz kommt. Neben der Berücksichtigung von räumlich-stochastischen Abhängigkeiten innerhalb einer Materialeigenschaft (Autokorrelation), ermöglicht der verwendete Ansatz auch die Einbeziehung von stochastischen Abhängigkeiten zwischen unterschiedlichen Materialeigenschaften (Kreuzkorrelation). Die räumlich streuenden Materialeigenschaften, z.B. Zugfestigkeiten, Verbundfestigkeiten und Elastizitätsmoduli werden den Stab- und Verbundelementen als Eigenschaften zugewiesen. Damit wird Heterogenität innerhalb sonst als homogen modellierter Materialien erreicht. Dies erzeugt Streuungen in den Ergebnissen ähnlich der Experimente.

Berechnungsergebnisse

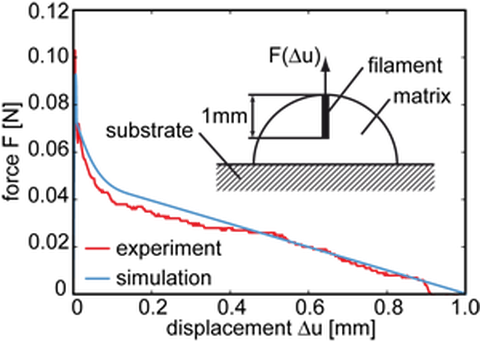
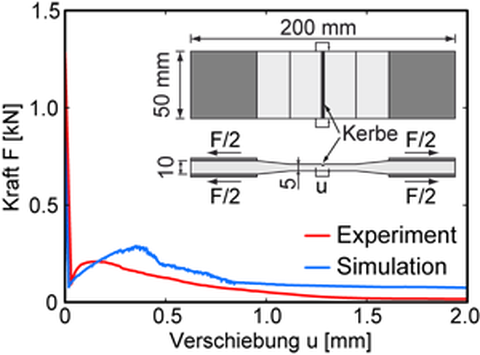
Das Modell ist in der Lage das Tragverhalten verschiedener einaxialer Zugversuche auf unterschiedlichen Skalen abzubilden. Beispielhaft seien hier der Filamentauszugversuch (Teilprojekt A5 (Mäder)), der Garnauszugversuch (Teilprojekt A6 (Mechtcherine)) und der Dehnkörperversuch (Teilprojekt B1 (Jesse)) genannt. Beispiele für simulierte Kraft-Verformungs-Beziehungen des Filamentauszugversuchs und des Garnauszugversuchs im Vergleich zu experimentellen Ergebnissen sind Abb. 4 dargestellt. Während die Übereinstimmung zwischen Simulation und Experiment für den Filamentauszugversuch zufriedenstellend gelingt, kann für den Garnauszugversuch bisher nur die qualitative Reproduktion der Trag- und Versagensmechanismen festgestellt werden. Es sind dafür also weitere Untersuchungen notwendig.

Abb. 4: Experimentelle und berechnete Kraft-Verformungsbeziehungen von Auszugversuchen: Kraft-Verformungs-
beziehung Filamentauszug (links), Kraft-Verfomungsbeziehung Garnauzug (rechts)

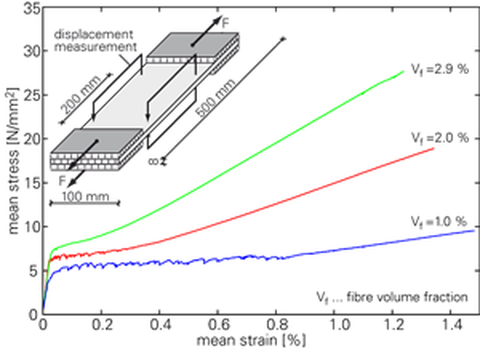
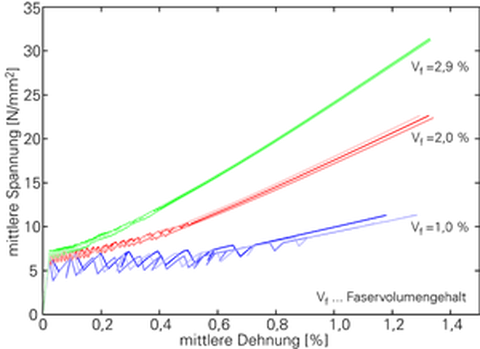
Der Fokus der Untersuchungen liegt auf den Dehnkörperversuchen des Teilprojektes B1 (Jesse), da hier realitätsnahe Bewehrungsgrade verwendet werden, die zu einer mehrfache Matrixrissbildung im Verbundwerkstoff führen. In Abb. 5 sind beispielhaft experimentell ermittelte und berechnete Spannungs-Dehnungsbeziehungen für verschiedene Bewehrungsgrade dargestellt.

Abb. 5: Experimentelle und berechnete Spannungs-Dehnungsbeziehungen:
Experimentelle Spannungs-Dehnungsbeziehungen (links), Berechnete Spannungs-Dehnungsbeziehungen (rechts)

Darüber hinaus kann das Modell Erkenntnisse über die im Experiment nicht oder nur schwer erfaßbare Spannungsverteilung im Inneren der Probekörper, z.B. in den Bewehrungsgarnen, erbringen. In Abb. 6 sind Spannungsverteilungen in der Matrix und der Bewehrung in Längsrichtung des Modells dargestellt. Dabei zeigt Abb. 6a Spannungsverteilungen bei einem Erstriss der Matrix. In Abb. 6b sind Spannungsverteilungen im Zustand der abgeschlossenen Rissbildung dargestellt. Wie zu erkennen ist, sind die äußeren Bereiche der Bewehrung im Rissquerschnitt am höchsten belastet. Zum Bewehrungskern hin nehmen die Normalspannungen ab. Zwischen den Rissen wird die Kraft durch Verbund wieder in die Matrix übertragen.

Abb. 6: Spannungsverteilungen im Mittelbereich (Meßbereich) der Probekörper: Spannungsverteilung im Matrixerstriss (links), Spannungsverteilung nach Abschluss der Rissbildung (rechts)

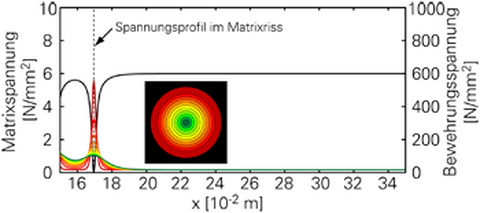
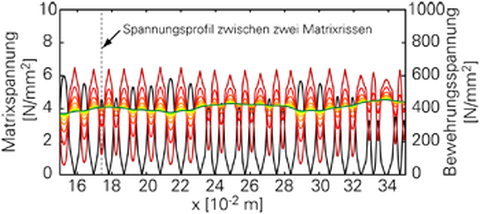
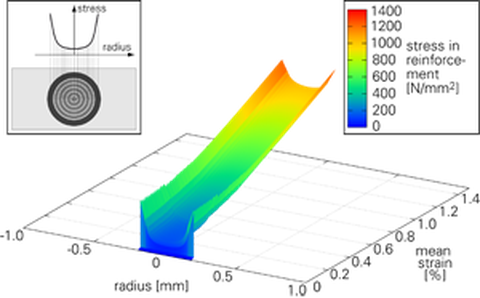
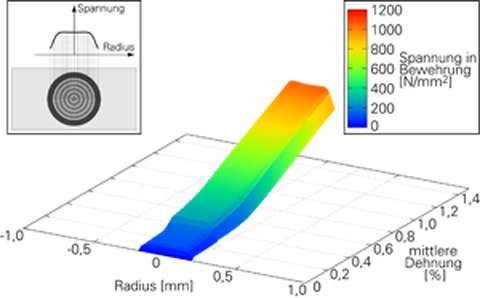
Unter steigender Belastung ändern sich auch die Spannungsprofile in der Bewehrung. Diese sind beispielhaft für einen Matrixrissquerschnitt und einen Querschnitt zwischen zwei Matrixrissen in Abb. 7 dargestellt. Im Matrixrissquerschnitt sind die Randschichten höher belastet als die Kernschichten (Abb. 7a). Im ungerissenen Bereich ist die Situation gerade umgekehrt (Abb. 7b). Die Spannungsprofile sind Eingangswerte für das Multiskalenmodell des Teilprojekts A3 (Zastrau).

Abb. 7: Spannungsprofile in der Bewehrung bei steigender äußerer Belastung: Im Matrixriss (links), Zwischen zwei Matrixrissen (rechts)

Darüber hinaus bietet das Modell die Möglichkeit weitere bemessungsrelevante Aspekte des Tragverhaltens des Verbundwerkstoffs textilbewehrter Beton in Abhängigkeit wechselnder Belastung zu untersuchen. Das Modell liefert z.B. Rissbreiten und -abstände, sowie Werte der Zugverfestigung. Außerdem kann der Einfluss eingeprägter Deformationen, z.B. resultierend aus Temperaturänderungen oder Schwinden der Matrix untersucht werden.

Schlussfolgerungen und Empfehlungen

Für eine realitätsnahe Simulation des Zugtragverhaltens von Textilbeton ist die Einbeziehung räumlich streuender Materialeigenschaften notwendig. Dabei beeinflussen streuende Matrixeigenschaften vorrangig die Matrixrissbildung, während streuende Bewehrungeigenschaften hauptsächlich das Versagensverhalten des Verbundwerkstoffs beeinflussen.
Die Ursache für das Steifigkeitsdefizit von Textilbeton im Zustand der abgeschlossenen Rissbildung ist auf eine Kombination von Effekten zurückzuführen. Dies sind aufgrund von Vorschädigung vorzeitig versagende Filamente, die Welligkeit der Filament, die für eine verzögerte Aktivierung und Streckung der Filamente sorgt, und das sukzessive Versagen der Multifilamentgarne in der Nähe des Traglastzustands.
Die Zugentfestigung der Matrix hat aufgrund der geringen Zuschlaggröße der Matrix speziell bei geringen Bewehrungsgraden einen untergeordneten Einfluß auf das Tragverhalten des Verbundwerkstoffs. Eine Erhöhung der Zähigkeit der Matrix, z.B. durch die Zugabe von Kurzfasern, kann jedoch sowohl eine Erhöhung der mittleren Steifigkeit im Zustand der Matrixrissbildung als auch einen Abbau von Spannungskonzentrationen in der Bewehrung in den Rissquerschnitten erbringen und damit eine Steigerung der Traglast des Verbundwerkstoffs erbringen.
Ein wesentliche Einflussfaktor auf die Zugversteifung ist die makroskopische Welligkeit der Bewehrungstextilien. Diese kann zu einer starker Vergrößerung der mittleren Dehnungen des Verbundwerkstoffs und damit sogenannter "negativer Zugversteifung" führen. Um diesen Effekt zu reduzieren ist eine möglicht gestreckte Ausrichtung der Garne im Textil von Vorteil, was durch den textilen Herstellungsprozess beeinflusst werden kann.
Durch eine Vergleichmäßigung der Spannungsverteilung zwischen Rand- und Kernfilamenten lässt sich das Festigkeitspotential der Multifilamentgarne besser ausnutzen und damit eine Erhöhung der Tragfähigkeit des Verbundwerkstoffs erzielen. Dafür ist eine Verbesserung des inneren Verbunds notwendig, wie sie bereits während der Laufzeit des SFB258 durch eine zusätzliche Beschichtung erzielt wurde.

Stellung innerhalb des Sonderforschungsbereichs

Mit seiner theoretischen Ausrichtung auf den mikroskopischen Betrachtungshorizont ist das Teilprojekt eng mit der Materialtechnologie, den experimentellen Untersuchungen und den theoretischen Untersuchungen auf Meso- und Makroebene verbunden. Im Einzelnen ergibt sich daraus die Zusammenarbeit mit den folgenden Teilprojekten.
Die Teilprojekte A6 (Mechtcherine) und B1 (Jesse) liefern Versuchsdaten zu unterbewehrten Zugversuchen mit einfacher Rissbildung bzw. Versuchen an Zugstäben mit mehrfacher Rissbildung. Auf der Grundlage umfangreicher Parameterstudien erhalten diese Projekte Hinweise zu noch offenen Problemstellungen, wie z.B. für die Modellierung notwendige, bisher noch nicht bestimmte Materialparameter (Bruchenergie der Matrix, Verbundeigenschaften). Darüber hinaus werden Hinweise zur möglichen Effizienzsteigerung gegeben.
Das Teilprojekt A3 (Zastrau) erhält zum einen Hinweise zum Materialverhalten auf der Mikroebene und zum anderen Berechnungsdaten in Form von lastabhängigen Spannungsverteilungen in der Bewehrung als Eingangswerte für die Mesoskala des Multiskalenmodells.
Das Teilprojekt B4 (Curbach) liefert Festigkeitsverteilungen und zugehörige Parameter für die Bewehrung. Außerdem werden an den Schnittstellen der Modellbildung die Berechnungsergebnisse gegenseitig kalibriert, um deren Plausibilität weiter zu untermauern.

Veröffentlichungen

2012

Hartig, J.; Jesse, F.; Schicktanz, K.; Häußler-Combe, U.: Influence of experimental setups on the apparent uniaxial tensile load-bearing capacity of Textile Reinforced Concrete specimens. Materials and Structures 45 (2012) 3, S. 433-446 - doi:10.1617/s11527-011-9775-0

2011

Hartig, J. U.: Numerical investigations on the uniaxial tensile behaviour of Textile Reinforced Concrete. Dresden : Technische Universität Dresden, Fakultät Bauingenieurwesen, Dissertation, 2011 – urn:nbn:de:bsz:14-qucosa-66614
Hartig, J.; Häußler-Combe, U.: A model for Textile Reinforced Concrete under imposed uniaxial deformations. In: Borkowski, A.; Lewinski, T.; Dzierzanowski, G. (Hrsg.): Proceedings of 19th International Conference on Computer Methods in Mechanics (CMM 2011). Warsaw : Warsaw University of Technology, 2011, S. 207-208 (Book of Short Papers) & Paper No. 133 CD of full papers - URL: http://www.cmm.il.pw.edu.pl/cd/pdf/133_f.pdf

2010

Hartig, J., Jesse, F.; Häußler-Combe, U.: Evaluation of Experimental Setups for Determining the Tensile Strength of Textile Reinforced Concrete. In: Brameshuber, W. (edt.): 2nd International Conference on Textile Reinforced Concrete (ICTRC2010), Proceedings of the International RILEM Conference on Material Science (MatSci). 6.-10.09.2010, RWTH Aachen. RILEM Publications S.A.R.L., Vol. 1, pp. 117-127
Hartig, J.; Häußler-Combe, U.: A model for the uniaxial tensile behaviour of Textile Reinforced Concrete with a stochastic description of the concrete material properties. In: Bicanic, N.; de Borst, R.; Mang, H.; Meschke, G. (eds.): Computational Modelling of Concrete Structures, Proceedings of the EURO-C 2010 in Rohrmoos/Schladming. London : Taylor & Francis, 2010, pp. 153-162
Hartig, J.; Häußler-Combe, U.: A model for the uniaxial tensile behaviour of textile reinforced concrete (TRC) covering effects at the micro and meso scales. In: Klingbeil, D.; Vormwald, M.; Eulitz, K.-G. (eds.): 18th European Conference on Fracture – Fracture of Materials and Structures from Micro to Macro Scale, 30.08-03.09.2010, TU Dresden. Deutscher Verband für Materialforschung und -prüfung e.V., Berlin, 2010, pp. 91 (Book of Abstracts) & CD of full papers
Hartig, J.; Häußler-Combe, U.: A model for the uniaxial tensile behaviour of textile reinforced concrete (TRC) covering effects at the micro and meso scales. In: Mechtcherine, V.; Kaliske, M. (eds.): Fracture and Damage of Advanced Fibre-reinforced Cement-based Materials. Aedificatio Publishers, Freiburg, 2010, pp. 213-221

2009

Hartig, J.; Häußler-Combe, U.: A model for Textile Reinforced Concrete exposed to uniaxial tensile loading. In: Kuczma, M. (Hrsg.); Wilmanski, K. (Hrsg.); Szajna, W. (Hrsg.): Proceedings of the 18th International Conference on Computer Methods in Mechanics – CMM2009, Zielona Góra, 18.–21.5.2009. Zielona Góra : The University of Zielona Góra Press, 2009, S. 203-204
Hartig, J.; Jesse, F.; Häußler-Combe, U.: Influence of different mechanisms on the constitutive behaviour of textile reinforced concrete. In: Curbach, M. (Hrsg.); Jesse, F. (Hrsg.): Textilbeton – Theorie und Praxis: Tagungsband zum 4. Kolloquium zu textilbewehrten Tragwerken (CTRS4) und zur 1. Anwendertagung, Dresden, 3.-5.6.2009. Dresden : Technische Universität Dresden, 2009, S. 157-168 URN: urn:nbn:de:bsz:14-ds-1244044908960-34481
Hartig, J.; Häußler-Combe, U.; Kitzig, M.: Effect of matrix tension softening on the uniaxial tensile behaviour of Textile Reinforced Concrete. In Smojver, I.; Soric, J. (Eds.): Proceedings of the 6th International Congress of Croatian Society of Mechanics (ICCSM), Dubrovnik, 30.9.-2.10.2009. Zagreb: Croatian Society of Mechanics, 2009, S. 46 (Book of Abstracts) & CD of full papers
Häußler-Combe, U.; Hartig, J.; Finzel, J.: Textilbeton-Sandwichbauteile – Tragverhalten unter Anpralllasten. In: Breit, W.; Schnell, J. & Grümann, R. (Hrsg.): Tagungsband zum Symposium: Lunar Base – Bauen für ein Leben auf dem Mond, 12.05.-13.05.2009, Kaiserslautern. TU Kaiserslautern & DLR, S. 61

2008

Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: Influence of bond properties on the tensile behaviour of Textile Reinforced Concrete. In: Cement and Concrete Composites 30 (2008) 10, p. 898-906 – doi:10.1016/j.cemconcomp.2008.08.004
Häußler-Combe, U.; Hartig, J.; Schicktanz, K.: An Approach for the Modelling of the Uniaxial Behaviour of Textile Reinforced Concrete. In: Schrefler, B. A.; Perego, U. (eds): 8th World Congress on Computational Mechanics (WCCM8) and 5th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2008) (CD of Abstracts), 30.06.-04.07.2008, Venice (Italy). Abstract 1415
Häußler-Combe, U.; Hartig, J.: Formulation and numerical implementation of a constitutive law for concrete with strain-based damage and plasticity. In: International Journal of Non-Linear Mechanics 43 (2008) 5, S. 399-415 – doi:10.1016/j.ijnonlinmec.2008.01.005

2007

Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: Modelling the uniaxial load-bearing behaviour of textile reinforced concrete with a lattice approach including damage. In: Triantafillou, T.C. (ed): Proceedings of the 8th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures (Book of short papers), 16.07.-18.07.2007, Patras (Greece). University of Patras, pp. 628-629
Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: Modelling the uniaxial load-bearing behaviour of textile reinforced concrete with a lattice approach including damage. In: Triantafillou, T.C. (ed): Proceedings of the 8th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures (CD of full papers), 16.07.-18.07.2007, Patras (Greece). University of Patras, Paper 17-2
Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: A lattice model approach to the uniaxial behaviour of Textile Reinforced Concrete. In: Carpinteri, A.; Gambarova, P.G.; Ferro, G.; Plizzari, G.A. (eds): Fracture Mechanics of Concrete and Concrete Structures (FraMCoS-6). Volume 2: Design, Assessment and Retrofitting of RC- Structures, 17.06.-22.06.2007, Catania (Italy). London : Taylor & Francis, pp. 745-752
Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: Zur Modellierung des einaxialen Zugtragverhaltens von textilbewehrtem Beton. In: Curbach, M.; Häußler-Combe, U.; Mechtcherine, V. (Hrsg.): Beiträge zum 48. Forschungskolloquium des DAfStb, 19.10.2007, Dresden. Technische Universität Dresden, S. 73-86
Häußler-Combe, U.; Hartig, J.: Bond and failure mechanisms of textile reinforced concrete (TRC) under uniaxial tensile loading. In: Cement and Concrete Composites 29 (2007) 4, p. 279-289 – doi:10.1016/j.cemconcomp.2006.12.012
Häußler-Combe, U.; Pröchtel, P.: Constitutive Laws for Concrete and their Application with Numerical Methods. In: Grosse, C.U. (eds): Advances in Construction Materials. 23.07.-24.07.2007, Stuttgart (Germany). Springer, pp. 31-38

2006

Curbach, M.; Schicktanz, K.; Jesse, F.; Hartig, J.: Stochastische Eigenschaften der Zugfestigkeit freier und zementös eingebetteter Filamentbündel aus AR-Glas. In: Neue Bauweisen – Trends in Statik und Dynamik, Tagungsband zum 10. Dresdner Baustatik Seminar, Technische Universität Dresden, 29.9.2006. S. 91-100
Häußler-Combe, U.; Hartig, J.; Schicktanz, K.: Numerische Modellierung des einaxialen Zugtragverhaltens von textilbewehrtem Beton. In: Neue Bauweisen – Trends in Statik und Dynamik, Tagungsband zum 10. Dresdner Baustatik Seminar, Technische Universität Dresden, 29.9.2006. S. 251-260
Häußler-Combe, U.; Hartig, J.: Structural behaviour of textile reinforced concrete. In: Meschke, G.; de Borst, R.; Mang, H.; Bicanic, N. (eds.): Computational Modelling of Concrete Structures, Proceedings of the EURO-C 2006 in Mayrhofen. Taylor&Francis Group, London, 2006, pp. 863-872
Häußler-Combe, U.; Hartig, J.: Uniaxial structural behaviour of TRC – A one-dimensional approach considering the transverse direction by segmentation. In: Hegger, J.; Brameshuber, W.; Will, N. (Hrsg.): Textile Reinforced Concrete – Proceedings of the 1st International RILEM Conference, 06.09.-07.09.2006, RWTH Aachen. RILEM, pp. 203-212

2005

Häußler-Combe, U. Jesse, F.: Rechnerische Untersuchungen zum einaxialen Tragverhalten von Textilbeton. Bauingenieur 80 (2005) 3, 131-141