Subproject B3
Numerische Untersuchungen zum Tragmechanismus von Filamentgarnen in einer Betonmatrix
Leitung
Prof. Dr.-Ing. habil. Ulrich Häußler-Combe
Institute of Concrete Structures
Mitarbeiter
Dr.-Ing. Jens Hartig
Dr.-Ing. Patrick
Pröchtel (ehemaliger Mitarbeiter)
Aim
The composite Textile Reinforced Concrete has with regard to
the matrix as well as the reinforcement a highly heterogeneous
structure. Existing modelling approaches on the macroscopic and
the mesoscopic scale, which assume that components of the
composite are homogeneous, are in principle able to reproduce
the global load-bearing behaviour. However, they are not
qualified to enhance the knowledge concerning the load-bearing
and failure behaviour, which originates from the microscopic
scale and which is not or only difficult ascertainable by means
of experiments. Existing microscopic models of Textile
Reinforced Concrete treat only the load-bearing behaviour of
homogeneous yarns and the load-carrying behaviour of the
composite at a solitary matrix crack. In view of the
load-bearing behaviour of structural elements made of Textile
Reinforced Concrete with multiple cracks, a demand for further
research becomes obvious.
The research program of the 1st project phase (3rd period of
CRC528) consists of the definition of a mechanical model
including the essential load-bearing mechanisms and system
parameters as well as the development of a respective numerical
model. For the validation of the model, different model
configurations corresponding to available experimental data of
filament pull-out tests, yarn pull-out tests and tension tests
with multiple cracking of the matrix shall be used. Based on
these model configurations, parametric studies shall be
performed, which shall lead to a better comprehension of the
bond mechanisms and the load-carrying and failure behaviour
arising thereof. This shall be the micro-mechanical basis for
the modelling on the mesoscopic and the macroscopic scale.
Furthermore, these investigations shall lead to recommendations
for efficiency enhancement of Textile Reinforced Concrete from
the viewpoint of concrete technology and textile
technology.
For the aspired model on the microscopic scale, firstly, the
relevant material and system parameters, e.g. the limited
tensile strengths for both the reinforcement and the matrix of
fine-grained concrete, for the load-bearing behaviour had to be
determined. Other material properties of the components of the
composite, as the heterogeneity and the fracture energy of the
matrix, were neglected in a first approach. In contrast, a
realistic representation of the reinforcement yarns with their
composition of a large number of filaments was assessed to be
necessary, also because of complex bond conditions inside the
yarns. Essentially, the bond inside a yarn can be distinguished
into an outer zone of adhesive bond where the filaments contact
the matrix and an inner zone where only small forces can be
transferred via adhesion at the contact areas of filaments,
which leads to a mostly frictional load transfer. Thus, a first
modelling approach is given with the subdivision of the yarns
into a sleeve zone and core zone.
Based on the results and insights of the first project phase,
which revealed certain deficiencies of the model developed so
far, an enhancement of the model seems to be necessary for the
2nd project phase (4th period of CRC528). It should include
tension softening of the matrix, waviness of the reinforcement
and spatial scatter of material parameters. By means of the
enhanced model further insight and recommendations for
improvement and optimisation of the composite shall be
provided. Moreover topics relevant for the design of structural
elements of Textile Reinforced Concrete as for instance the
interaction between steel reinforced concrete and Textile
Reinforced Concrete as well as the load-bearing behaviour due
to imposed loading is intended.
Results
Model
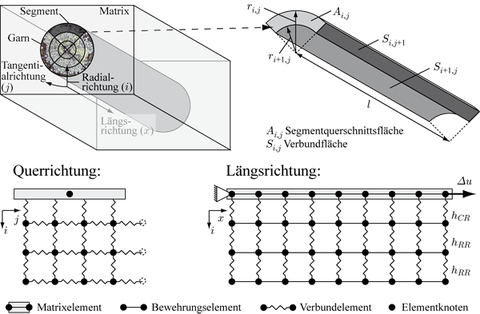
The basis of the mechanical model is the so-called segment model, see Fig. 1, from which also the numerical model is derived after discretisation with the Finite Element Method. Therefore, the reinforcement is subdivided into segments (Fig. 1, top left), which are assumed to be homogeneous, and, which are arranged in a regular lattice scheme (Fig. 1, bottom left). The matrix is also assumed homogeneous over the cross section perpendicular to the loading direction. The behaviour of the segments in longitudinal direction is approximated by bar elements, which act according to uniaxial material laws neglecting transverse effects, e.g. due to Poisson's ratio, and have a cross-sectional area as geometrical property. The cross-sectional areas of the matrix bar elements correspond to the cross-sectional area of the specimen while the cross-sectional areas of the reinforcement bar elements are determined by the the segmentation approach. In longitudinal direction a large number of bar elements are arranged in series (Fig. 1, bottom right), in order to cover the multiple cracking behaviour of matrix and reinforcement and the bond behaviour between the segments realistically.
Fig. 1: Geometric model and segment discretization
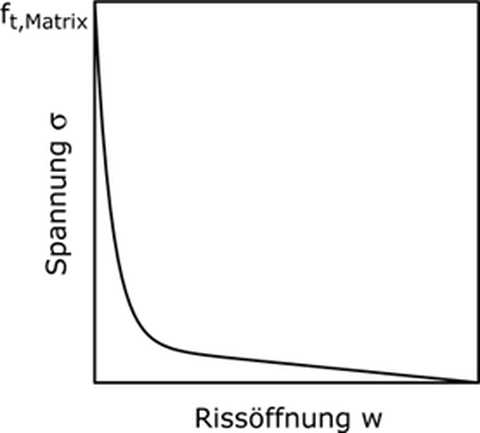
The material behaviour of the matrix is assumed linear
elastic according to the Young's modulus with a tensile
strength limit. After exceeding of the tensile strength,
brittle failure can be assumed in a first approach. More
realistic is considering tension softing, which is modelled
with a stress-crack width relation (Fig. 2a). A respective
stress-strain relation results from a regularisation based on
the crack band approach.
The material behaviour of the reinforcement can be also assumed
linear elastic up to a tensile strength limit in a first
approach. However, experiments show often a delayed activation
of the reinforcement caused by a waviness of the reinforcement.
This geometrical effect on small scale is considered in the
material law by a successive transition to the linear course of
the stretched reinforcement (Fig. 2b).
Fig. 2: Material laws for matrix and reinforcement: Tension softening law for matrix (left), Material law with delayed activation for reinforcement (right)
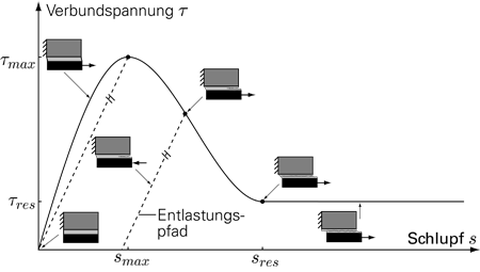
The bar elements chains are connected at element nodes via bond elements. The geometric property of a bond element is described with a bond area, which is derived from the segment model (Fig. 1, top right). The reduction of bond area in the case of fibre pullout can be taken into account in the model by the determination of the bond area depending on the position of a bond element to cracked concrete bar elements. The definition of the bond characteristics is performed by means of bond stress-slip relations (Fig. 3), which are assigned to the bond elements as material laws. The input parameter is the slip s, which results from the relative displacement of both nodes of a bond element. From the slip s the bond stress τ of the element can be calculated. The course of the bond law is defined by supporting points (s, τ) with interpolation in between. Therefore, the so-called "Piecewise Cubic Hermite Interpolating Polynomial" (PCHIP) consisting of special cubic polynomials is used, which show monotonicity and continuity on an interval in their first derivatives. This reduces numerical problems during computations on the transition between the function intervals of the bond law. An important aspect regarding bond modelling is the behaviour in case of unloading. In the bond law, the unloading path differs from the loading path and takes inelastic deformations into account.
Fig. 3: Bond stress-slip relation
Simulation results
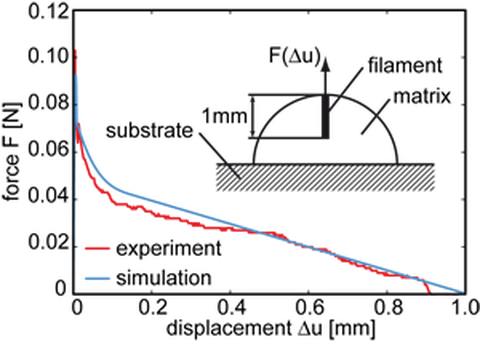
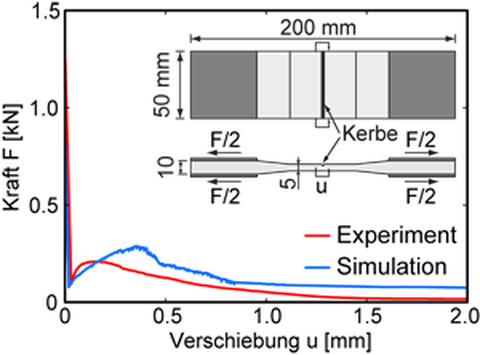
The model is able to reproduce the global load-bearing behaviour of various uniaxial tension tests on different scales as for instance the filament pull-out test (subproject A5 (Mäder)), the yarn pull-out test (subproject A6 (Mechtcherine)) and the tension test with multiple matrix cracking (subproject B1 (Jesse)). Examples of simulated force-deformation relations of the filament pull-out test and the yarn pull-out test in comparison with experimental results are shown in Fig. 4. While the correspondence between simulated and experimental results is satisfactory for the filament pull-out test, the results of the yarn pull-out tests show hitherto only a qualitative reproduction of the load-bearing and failure mechanisms. Therefore, further investigations are necessary.
Fig. 4: Experimental und simulated force-displacement relation of pull-out tests: Experimental stress-strain relations (experimental data: subproject B1 (Jesse)) (left), Simulated stress-strain relations (right)
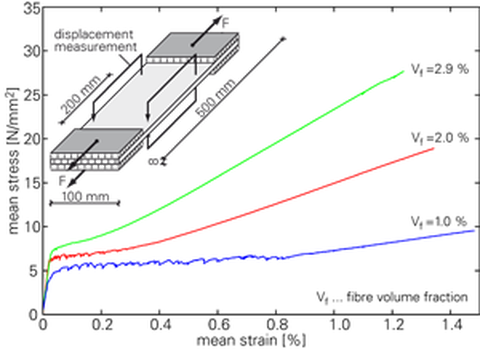
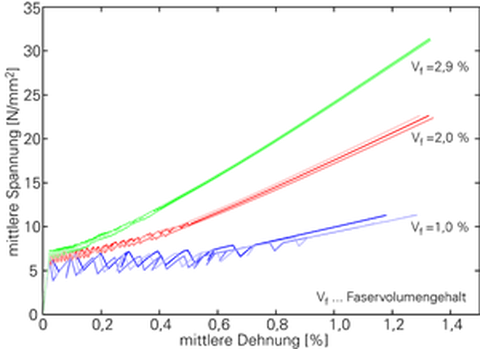
The investigations were focussed on the tension tests with multiple matrix cracking by subproject B1 (Jesse), because in these tests reinforcement ratios as used in practice are applied. In Fig. 5, exemplary experimental and simulated stress-strain relations with different fibre volume fractions are shown.
Fig. 5: Experimental and simulated stress-strain relations:Experimental stress-strain relations (experimental data: subproject B1 (Jesse)) (left), Simulated stress-strain relations (right)
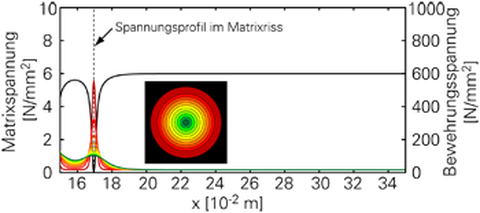
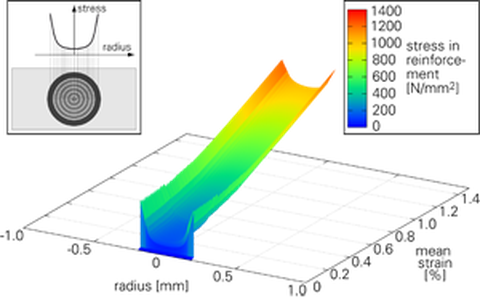
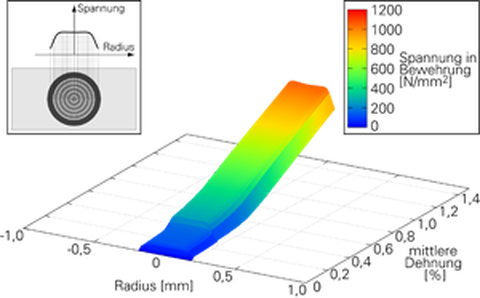
Furthermore, the model is able to give insight into the stress distribution inside a specimen, e.g. in a reinforcement yarn, which is not or only difficult ascertainable in experiments. In Fig. 6, the stress distributions in matrix and reinforcement in longitudinal direction of the model are presented. Fig. 6a shows stress distributions at a single crack and Fig. 6b in the stabilised cracking state. It can be seen that the outer layers of the reinforcement have the highest stresses in the cracked cross section. Towards the core of the reinforcement, the normal stresses decrease. The force is transferred back to the matrix between the cracks by bond mechanisms.
Fig. 6: Stress distribution in the centre part of the
specimen: Stress distribution at a primary crack of the matrix
(left), Stress distribution in the final state of the matrix
(right)
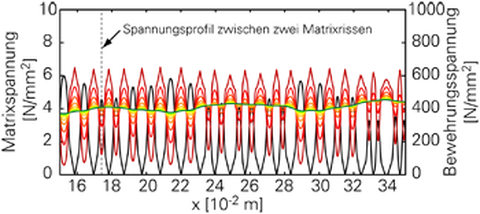
With increasing loads, the stress profiles in the reinforcement change. In Fig. 7, the stress distributions in the cross section of a matrix crack and a cross section between two matrix cracks are shown exemplarily. At the matrix crack, the sleeve segment is higher loaded as the core segments (Fig. 7a). In the zone between two cracks, the situation is vice versa (Fig. 7b). These stress profiles are also input for the multi-scale model of subproject A3(Zastrau).
Fig. 7: Stress profile in the reinforcement with increasing external loading: At the matrix crack (left), Between two matrix cracks (right)
Conclusions and recommendations
- For a realistic simulation of the tensile load-bearing behaviour of Textile Reinforced Concrete consideration of spatially scattering material properties is necessary. Scattering matrix properties influence primarily the multiple matrix crack development while scattering reinforcement properties control primarily the failure behaviour of the composite.
- The stiffness deficit of Textile Reinforced Concrete in the stabilised cracking state results from several sources. These are pre-damaged filaments failing on low load levels, the waviness of the reinforcement leading to a delayed activation and stretching of the filaments and the successive failure of the multi-filament yarns close to the ultimate state.
- Tension softening of the matrix has due the small aggregates of the matrix small influence on the load-bearing behaviour of the composite, especially with low reinforcement ratios. An increase of matrix toughness, e.g. by means of short fibre addition, might lead to an increase of mean stiffness in the state of multiple matrix cracking as well as a reduction of stress concentrations in der reinforcement at the cracks leading to increasing ultimate stresses of the composite.
- The macroscopic waviness of the textile reinforcement has considerable influence on tension stiffening of the composite. It can lead to a strong increase of mean composite strains and so-called "negative tension stiffening". To reduce this effect a stretched alignment of the yarns in the textile is advantagous. This can be influenced during textile processing.
- The strength potential of the multi-filament yarns can be better exploited by a homogenisation of the stress distribution between sleeve and core filaments. This would lead also to a higher load-bearing capacity of the composite. Therefor, an improvement of the inner bond is necessary, which can be achieved by means of an additional coating of the reinforcement as already performed during the previous periods of CRC528.
Position in the collaborative research centre
Due to its theoretical orientation at the microscopic scale,
the subproject is close related with the material technology,
the experimental investigations and the theoretical
investigations at mesoscopic scale and the macroscopic scale.
In detail, the following cooperation with other subprojects
exists.
The subprojects A6 (Mechtcherine) and B1 (Jesse) provide
experimental results of tension tests with a single matrix
crack and tension tests with multiple matrix cracking
respectively. These subprojects receive information based on
extensive parametric studies about open questions, as for
instance undetermined parameters (fracture energy, bond
properties), which are necessary for the modelling.
Furthermore, advices are given concerning a possible increase
of efficiency of the interplay between matrix and
reinforcement.
The subproject A3 (Zastrau) receives information concerning the
material behaviour at the microscopic scale and results of
simulations in the form of load-dependent stress distributions
in the reinforcement as input values for the mesoscopic scale
of the multi-scale model.
The subproject B4 (Curbach) provides strength distributions and
associated parameters for the reinforcement. Furthermore, the
results of the simulations are mutually calibrated at the
contact points of modelling in order to substantiate their
plausibility.
Publications
2011
- Hartig, J. U.: Numerical investigations on the uniaxial tensile behaviour of Textile Reinforced Concrete. Dresden : Technische Universität Dresden, Fakultät Bauingenieurwesen, Dissertation, 2011 – urn:nbn:de:bsz:14-qucosa-66614
- Hartig, J.; Häußler-Combe, U.: A model for Textile Reinforced Concrete under imposed uniaxial deformations. In: Borkowski, A.; Lewinski, T.; Dzierzanowski, G. (Hrsg.): Proceedings of 19th International Conference on Computer Methods in Mechanics (CMM 2011). Warsaw : Warsaw University of Technology, 2011, S. 207-208 (Book of Short Papers) & Paper No. 133 CD of full papers - URL: http://www.cmm.il.pw.edu.pl/cd/pdf/133_f.pdf
2010
- Hartig, J., Jesse, F.; Häußler-Combe, U.: Evaluation of Experimental Setups for Determining the Tensile Strength of Textile Reinforced Concrete. In: Brameshuber, W. (edt.): 2nd International Conference on Textile Reinforced Concrete (ICTRC2010), Proceedings of the International RILEM Conference on Material Science (MatSci). 6.-10.09.2010, RWTH Aachen. RILEM Publications S.A.R.L., Vol. 1, pp. 117-127
- Hartig, J.; Häußler-Combe, U.: A model for the uniaxial tensile behaviour of Textile Reinforced Concrete with a stochastic description of the concrete material properties. In: Bicanic, N.; de Borst, R.; Mang, H.; Meschke, G. (eds.): Computational Modelling of Concrete Structures, Proceedings of the EURO-C 2010 in Rohrmoos/Schladming. London : Taylor & Francis, 2010, pp. 153-162
- Hartig, J.; Häußler-Combe, U.: A model for the uniaxial tensile behaviour of textile reinforced concrete (TRC) covering effects at the micro and meso scales. In: Klingbeil, D.; Vormwald, M.; Eulitz, K.-G. (eds.): 18th European Conference on Fracture – Fracture of Materials and Structures from Micro to Macro Scale, 30.08-03.09.2010, TU Dresden. Deutscher Verband für Materialforschung und -prüfung e.V., Berlin, 2010, pp. 91 (Book of Abstracts) & CD of full papers
- Hartig, J.; Häußler-Combe, U.: A model for the uniaxial tensile behaviour of textile reinforced concrete (TRC) covering effects at the micro and meso scales. In: Mechtcherine, V.; Kaliske, M. (eds.): Fracture and Damage of Advanced Fibre-reinforced Cement-based Materials. Aedificatio Publishers, Freiburg, 2010, pp. 213-221
2009
- Hartig, J.; Häußler-Combe, U.: A model for Textile Reinforced Concrete exposed to uniaxial tensile loading. In: Kuczma, M. (Hrsg.); Wilmanski, K. (Hrsg.); Szajna, W. (Hrsg.): Proceedings of the 18th International Conference on Computer Methods in Mechanics – CMM2009, Zielona Góra, 18.–21.5.2009. Zielona Góra : The University of Zielona Góra Press, 2009, S. 203-204
- Hartig, J.; Jesse, F.; Häußler-Combe, U.: Influence of different mechanisms on the constitutive behaviour of textile reinforced concrete. In: Curbach, M. (Hrsg.); Jesse, F. (Hrsg.): Textilbeton – Theorie und Praxis: Tagungsband zum 4. Kolloquium zu textilbewehrten Tragwerken (CTRS4) und zur 1. Anwendertagung, Dresden, 3.-5.6.2009. Dresden : Technische Universität Dresden, 2009, S. 157-168 URN: urn:nbn:de:bsz:14-ds-1244044908960-34481
- Hartig, J.; Häußler-Combe, U.; Kitzig, M.: Effect of matrix tension softening on the uniaxial tensile behaviour of Textile Reinforced Concrete. In Smojver, I.; Soric, J. (Eds.): Proceedings of the 6th International Congress of Croatian Society of Mechanics (ICCSM), Dubrovnik, 30.9.-2.10.2009. Zagreb: Croatian Society of Mechanics, 2009, S. 46 (Book of Abstracts) & CD of full papers
- Häußler-Combe, U.; Hartig, J.; Finzel, J.: Textilbeton-Sandwichbauteile – Tragverhalten unter Anpralllasten. In: Breit, W.; Schnell, J. & Grümann, R. (Hrsg.): Tagungsband zum Symposium: Lunar Base – Bauen für ein Leben auf dem Mond, 12.05.-13.05.2009, Kaiserslautern. TU Kaiserslautern & DLR, S. 61
2008
- Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: Influence of bond properties on the tensile behaviour of Textile Reinforced Concrete. In: Cement and Concrete Composites 30 (2008) 10, p. 898-906 – doi:10.1016/j.cemconcomp.2008.08.004
- Häußler-Combe, U.; Hartig, J.; Schicktanz, K.: An Approach for the Modelling of the Uniaxial Behaviour of Textile Reinforced Concrete. In: Schrefler, B. A.; Perego, U. (eds): 8th World Congress on Computational Mechanics (WCCM8) and 5th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2008) (CD of Abstracts), 30.06.-04.07.2008, Venice (Italy). Abstract 1415
- Häußler-Combe, U.; Hartig, J.: Formulation and numerical implementation of a constitutive law for concrete with strain-based damage and plasticity. In: International Journal of Non-Linear Mechanics 43 (2008) 5, S. 399-415 – doi:10.1016/j.ijnonlinmec.2008.01.005
2007
- Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: Modelling the uniaxial load-bearing behaviour of textile reinforced concrete with a lattice approach including damage. In: Triantafillou, T.C. (ed): Proceedings of the 8th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures (Book of short papers), 16.07.-18.07.2007, Patras (Greece). University of Patras, pp. 628-629
- Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: Modelling the uniaxial load-bearing behaviour of textile reinforced concrete with a lattice approach including damage. In: Triantafillou, T.C. (ed): Proceedings of the 8th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures (CD of full papers), 16.07.-18.07.2007, Patras (Greece). University of Patras, Paper 17-2
- Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: A lattice model approach to the uniaxial behaviour of Textile Reinforced Concrete. In: Carpinteri, A.; Gambarova, P.G.; Ferro, G.; Plizzari, G.A. (eds): Fracture Mechanics of Concrete and Concrete Structures (FraMCoS-6). Volume 2: Design, Assessment and Retrofitting of RC- Structures, 17.06.-22.06.2007, Catania (Italy). London : Taylor & Francis, pp. 745-752
- Hartig, J.; Häußler-Combe, U.; Schicktanz, K.: Zur Modellierung des einaxialen Zugtragverhaltens von textilbewehrtem Beton. In: Curbach, M.; Häußler-Combe, U.; Mechtcherine, V. (Hrsg.): Beiträge zum 48. Forschungskolloquium des DAfStb, 19.10.2007, Dresden. Technische Universität Dresden, S. 73-86
- Häußler-Combe, U.; Hartig, J.: Bond and failure mechanisms of textile reinforced concrete (TRC) under uniaxial tensile loading. In: Cement and Concrete Composites 29 (2007) 4, p. 279-289 – doi:10.1016/j.cemconcomp.2006.12.012
- Häußler-Combe, U.; Pröchtel, P.: Constitutive Laws for Concrete and their Application with Numerical Methods. In: Grosse, C.U. (eds): Advances in Construction Materials. 23.07.-24.07.2007, Stuttgart (Germany). Springer, pp. 31-38
2006
- Curbach, M.; Schicktanz, K.; Jesse, F.; Hartig, J.: Stochastische Eigenschaften der Zugfestigkeit freier und zementös eingebetteter Filamentbündel aus AR-Glas. In: Neue Bauweisen – Trends in Statik und Dynamik, Tagungsband zum 10. Dresdner Baustatik Seminar, Technische Universität Dresden, 29.9.2006. S. 91-100
- Häußler-Combe, U.; Hartig, J.; Schicktanz, K.: Numerische Modellierung des einaxialen Zugtragverhaltens von textilbewehrtem Beton. In: Neue Bauweisen – Trends in Statik und Dynamik, Tagungsband zum 10. Dresdner Baustatik Seminar, Technische Universität Dresden, 29.9.2006. S. 251-260
- Häußler-Combe, U.; Hartig, J.: Structural behaviour of textile reinforced concrete. In: Meschke, G.; de Borst, R.; Mang, H.; Bicanic, N. (eds.): Computational Modelling of Concrete Structures, Proceedings of the EURO-C 2006 in Mayrhofen. Taylor&Francis Group, London, 2006, pp. 863-872
- Häußler-Combe, U.; Hartig, J.: Uniaxial structural behaviour of TRC – A one-dimensional approach considering the transverse direction by segmentation. In: Hegger, J.; Brameshuber, W.; Will, N. (Hrsg.): Textile Reinforced Concrete – Proceedings of the 1st International RILEM Conference, 06.09.-07.09.2006, RWTH Aachen. RILEM, pp. 203-212
2005
- Häußler-Combe, U. Jesse, F.: Rechnerische Untersuchungen zum einaxialen Tragverhalten von Textilbeton. Bauingenieur 80 (2005) 3, 131-141