Slopes
Embankments can be found for example near the coast in the form of dikes, along traffic routes in the form of noise protection walls or in sloped excavation pits. The stability of these earthworks is always essential. The safety against failure can be estimated for different scenarios with the help of analytical and numerical approaches. However, for all methods a value for the shear strength of the in-situ soil has to be prescribed. The shear strength is coupled with the displacement and mobilized shear stress, which is not taken into account in the calculation approaches.
For very large slopes such as in an open-pit mine, the stability calculations are demanding because of complex geological and hydrological conditions. Therefore, the slopes are monitored with measuring systems to obtain information on displacements and changes in pore water pressure, which can be additionally included in the calculations.
Measured displacements in a slope system or calculated displacements by means of numerical methods are often evaluated with regard to the early detection of failure. At the Institute of Geotechnical Engineering it has been investigated whether displacements or the combination of displacements in different points in a slope system can also be used for the recognition of processes (e.g. dissipation of negative and positive excess pore water pressure, creep, progressive failure, etc.) in the ground. Here, the focus lay on displacements during and after slope excavation. Numerical excavation simulations were carried out, which considered different processes such as the consolidation after an undrained excavation or a groundwater lowering with subsequent excavation. The obtained displacements were compared and evaluated in terms of characteristic and recognizable patterns.
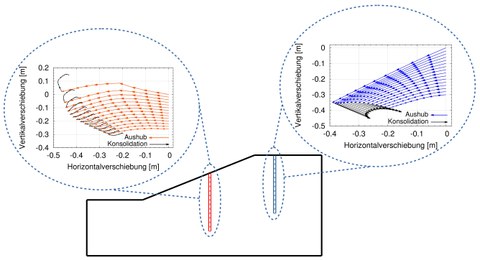
Displacement patterns in a slope due to undrained excavation and subsequent consolidation
For an idealized slope in homogeneous soil, explicit recognition features were determined, i.e. processes in the ground can be identified by displacement patterns.
The evaluation of measured displacements in field tests and the comparison with already identified displacement patterns is planned.
Many calculation methods for the determination of slope stability assume a limit equilibrium, i.e. a state of equilibrium between the acting and resisting forces within a slope system. The acting forces are determined basedon thespecific weight of the potential slip body as well as surcharges etc. The resisting forces are calculated assuming a failure criterion, usuallythe Mohr-Coulomb model. The used shear parameters (friction angle φ', cohesion c') reflect the maximum shear strength of the soil. However, laboratory tests show that a deformation has to take place until the maximum shear strength is mobilized. This deformation is neglected in stability calculations. For soils which tend to softening, the assumption of the peak shear strength for stability calculations may overestimate the safety. This is due to the fact that the maximum shear strength is not attained simultaneouslyin all points along the potential slip surface.
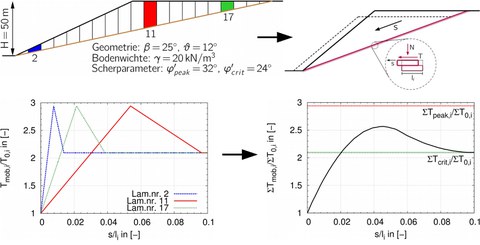
Qualitative development of the shear strength for single slices in the slope system and mobilized global shear strength in dependence on shearing
The developed method uses numerical element test calculationsto determine the evolution of the mobilized shear strength as a function of shear strain in points along a slip surface. The integration of the mobilized shear strength in dependence of shear strain in all points leads to a strain-dependent slope stability.
For the calculation of the slope stability, in general the friction angle φ' and the cohesion c' (shear strength in the stress-free state) are used to determine the shear resistance. These parameters are derived from laboratory tests, soil-specific and are subjected to certain fluctuations, which can be statistically recorded. Based on a statistical parameter distribution, the slope stability for varying parameters can be calculated and a level of safety can be deduced. The scientific correlation between the statistical distribution of shear parameters and the level of slope stability has not been completely clarified and is therefore being investigated in more detail.
