DEM simulations of multiaxial failure mechanisms
Table of contents
Project data
|
Titel | Title |
Report in the annual report 2019
DISCRETE ELEMENT SIMULATION OF CONCRETE‘S MATERIAL BEHAVIOUR IN 3D

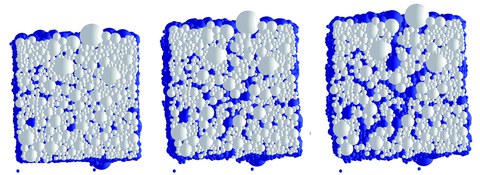
Virtual concrete specimen – paricle ensemble with varying sphere diameters
The material and damage behaviour of concrete using discrete element method (DEM) is investigated in this project. A simulation with spherical particles is used. The enormous advantage of spherical particles is that only the particle’s centre and diameter are required for the entire particle description. Furthermore, the contact detection is simplified substantially. The check, whether two neighbouring particles do actually contact or overlap each other, leads to much lower calculation costs than for polygonally shaped particles. This check of contact or overlap, respectively, needs to be done in every time step to calculate the repulsive force. However, spherical particles have the disadvantage, that no form closure is enabled and that an additional cohesive force is mandatorily required to keep the particles as a whole assembly.
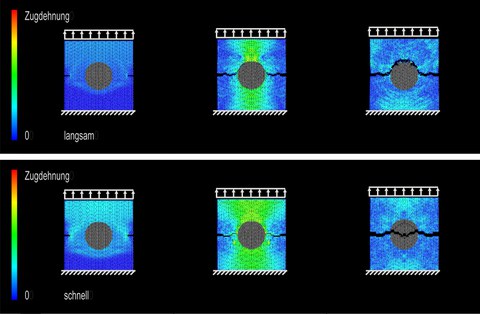
Numerical Simulation of multiaxial damage behaviour of concrete using Discrete Element Method
In the simulation, particle configurations with varying particle radii as well as with constant radius are investigated. A virtual test specimen is generated by randomly mixing a requested number of spheres of different size and by pouring the spherical bulk ensemble into the simulation space. This generates a particle configuration representing concrete test specimen as the result of the pre-processing procedure. The particle radii used are chosen according to a real grain-size distribution curve of concrete, i. e. they represent aggregates of varying sizes. Using particles of the same particle radius on contrast, this always leads to a hexagonal particle formation as the densest packing configuration. This simplification of the particle model reduces the calculation costs significantly. Using this model type, simulations of uniaxial tensile load and the crack growth under varying loading velocities are investigated. It is in special focus, whether a crack develops around an aggregate, or whether the crack goes through an aggregate. This means either the aggregate remains in its original size or it is broken up. The simulation shows that the crack grows around an aggregate under lower loading velocity, and the crack breaks up the aggregate under higher velocities.
Report in the annual report 2018
DEM - CONTINUOUSLY DISCONTINUOS

Festbetonprobekörper nach dem Spallationsversuch am Hopkinson-Bar
Die uns umgebende Welt ist diskontinuierlich, voller Lücken und diskret, das Kontinuum nur eine – allerdings sehr praktische – Vereinfachung. Dabei erfordert diese Vereinfachung einen umfangreichen mathematischen Apparat und einen enormen Sachverstand, um auch nur einfachste Geometrien und Materialannahmen numerisch abbilden zu können. Vielfach, nein: in aller Regel ist man am Ende doch wieder darauf angewiesen, Raum und Zeit zu diskretisieren und dem Computer die Lösung der Gleichungen zu überlassen.
Die Methode der diskreten Elemente (DEM) gehört zur Kategorie der partikelbasierten Methoden. Sie vermeidet den „Umweg“ über die Kontinuumsmechanik und arbeitet direkt mit den der Teilchen-Teilchen-Wechselwirkung zugrundeliegenden Phänomenen. Die Newtonschen Bewegungsgleichungen bilden dabei gleichsam das Fundament, auf dem und um das herum geeignete Bausteine zur Beschreibung von Formschluss, Kohäsion und Reibung angeordnet werden. Kinematik und Dynamik sind hier keine hinzuzufügenden „Features“, sondern inhärenter Teil der Methode.

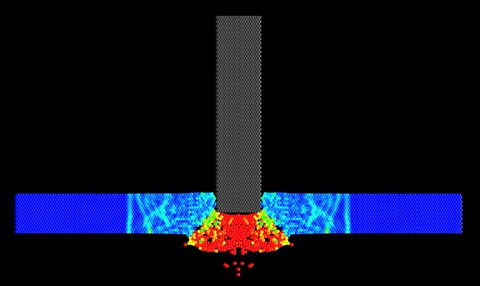
Virtueller Betonprobekörper für den numerischen Spallationsversuch
Im Spallationsversuch – der kurzen, schockartigen Belastung eines Festkörpers mit bekannten statischen Materialeigenschaften durch einen Impaktor oder ein Projektil – treffen die verschiedenen Welten aufeinander: die körnige und die kontinuierliche, die statische und die dynamische. Er stellt eine Schnittstelle dar zwischen der diskreten mesoskopischen Ebene von Zementmatrix und Zuschlagkorn und der makroskopischen Welt, in der wir leben und bauen. Gleichzeitig ist er ein ausgezeichnetes Versuchsfeld zum Studium unterschiedlicher numerischer Methoden.
Der virtuelle Spallationsversuch war einer der Schwerpunkte dieses von der Deutschen Forschungsgemeinschaft geförderten Projekts. Die einzelnen Schritte der Simulation bestehen dabei zunächst in der Generierung des virtuellen Probekörpers („Mischen“ und „Aushärten“) und der Modellierung der anderen am virtuellen Experiment beteiligten Objekte. Anschließend werden der Simulationsraum konfiguriert und die Objekte darin positioniert und initialisiert („Einspannen“, „Laden“). Wie im Labor versetzt man sich daraufhin in die Rolle des Beobachters und verzeichnet die im Simulationsraum sich ergebenden Phänomene („Messen“). Auf diese Weise hoffen wir, das Laborexperiment besser verstehen zu können, Nicht-Sichtbares sichtbar zu machen und weitere reale oder virtuelle Experimente besser planen zu können.
Report in the year book 2017
THE STRAIN RATE EFFECT – STRAIN, STRESS OR JUST INERTIA?

Virtual aggregate inside of cementitious matrix – tensile test at low strain rate; the crack propagates, beginning from the notch …
Postulated and confirmed by experiments, then again simply called a myth – the so-called strain rate effect is a permanent subject of the argument amongst theorists as well as practitioners in the field of concrete’s material behaviour. This terminus technicus is used to describe the actual or supposed increase of material strength at high strain rates that appear in situations of shock and impact – one may think of natural events like earthquakes or rock fall, of high-mass accidents, but also of the disastrous effect of explosions and projectile motion.
It is not the individual experimental set-up or the raw experimental data that frequently raise questions, but the interpretation of the experimental results and the different ways to explain data by different phenomena. Some researchers challenge the effect as a sheer effect of inertia, others accept it as being partially substantial.
One common explanation makes the increasing number of crushed aggregates at high strain rates responsible for the phenomenon called strain rate effect.
Situations of shock and impact are characterized by a high degree of suddenness, which, in the past, made it a great challenge to investigate dynamic material behaviour. Nowadays semiconductor-based strain gauges and piezo-electric accelerometers are available that allow to study the spatial and temporal aspects of wave propagation at high resolution. Now again, the researcher is confronted by another problem: Since high-resolution gauges are applied at different points of the respective specimen, different information is obtained twice at the same time – an effect which is called time lag. It is the old conundrum of the man who owns two watches: He’ll never know how late it is.
Numerical simulations can help to make the numerous effects of wave propagation and crack evolution visible and therefore easier to understand. They are not intended to replace, but to accompany experiments in a useful and very practical manner that allows the interpretation and extrapolation of experimental data. The discrete element method (DEM) seems to be extremely suitable to deal with several effects of shock wave propagation and material behaviour at high strain rates. Since almost completely based on Newton’s laws of motion, inertial effects are intrinsic elements of the computational method which can be estimated in qualitative and quantitative manner – or completely neglected.
Report in the year book 2016
Simulation of pull-out tests using discrete element method

Virtual pull out-test with ca. 9,000 particles before (initial position) and at the beginning of the test, i.e. shortly after the sudden acceleration has been applied to the reinforcement bar. Blue = particles without velocity, red = particles with high velocity
Reinforced concrete is able to take a load only if concrete and reinforcement steel work together properly and if the bonding of both components is ensured.
In order to investigate the anchoring or bonding of the steel reinforcement bar, so-called pull-out tests are done in laboratory experiments. With regard to parameter studies, it is convenient to model such pull-out tests using numerical simulations. In this research project based on discrete element method, the bonding between reinforcement steel and concrete is numerically investigated in virtual pull-out tests using cubic and cylindrical virtual test specimens. The aim is not primarily to model the geometric conditions of real steel reinforcement bars. But the aim is rather to investigate the potential of the discrete element method for pull-out test. The simulations are done for pull-out tests under quasi-static and under high-dynamic loading conditions. For this purpose, the 3D simulation code using particles of equal size and spherical shape is used which leads to a hexagonally dense packing of the particle ensemble. The test specimen is represented by an ensemble of particles. The forces are transmitted interactively via contacting, neighbouring particles. Different material parameters are used for the particles of the concrete body and of the reinforcement steel. The bonding of the concrete and the reinforcement bar is modeled using a combining rule for the bonding zone (the Lorentz-Berthelot rule in our case) and above all using the geometrical toothing of the rebar ribs in the concrete material.
The simulation is able to show the wave propagation in the virtual test specimen. The typical forward-facing impact cones spread within the neighbouring concrete material.
The force interaction can be modeled in the zones of geometrical toothing and the simulation is able to show also the cracks and holes at the back-side of the rebar ribs which are also observed in real laboratory experiments – these two facts show the great potential of the discrete element method regarding numerical simulations of pull-out tests.
Report in the year book 2015
Concrete – some kind of transparency
Numerical simulation: the visualization shows the characteristic cone of expelled material and shock wave propagation inside the virtual specimen
Besides its well-known static properties, which make concrete the most commonly used material for massive construction, this material offers a fascinating variety of dynamic effects which are of both theoretical and very practical interest – one may think of earthquakes, high-mass accidents or impact situations. Such situations are characterized by extreme suddenness, caused by the brief duration of the loading itself, as well as by the high velocity of shock wave propagation and crack evolution inside of the material or the structure exposed to the sudden heavy loading.
However, it is a challenging task to investigate impact situations in the laboratory. Not only does it take some effort to generate such situations at full-scale – a drop tower, the split-Hopkinson pressure bar and other devices are complex man-made constructions which have to be designed, built, run and maintained. Often enough, it is also not clear where and when the phenomena of interest will occur inside of the respective specimen and how the experimental results obtained by the applied sensors and gauges are to be interpreted and extrapolated.
Numerical simulations can help to make the material a little more transparent. They allow – at least in a qualitative manner – to get an idea, to get a picture of phenomena like shock wave propagation, crack evolution and spallation. Discrete element simulations avoid understanding and describing concrete as a continuum. They take into consideration the material’s heterogeneity and allow the virtual aggregates and/or cement particles to interact, to lose contact and to re-interact at each stage of the simulation. Phenomena like wave propagation and crack evolution, spalling effects and even cones of material being expelled from the virtual specimen emerge in a quite natural way. In the course of this research project, we try to investigate the quasi static and the dynamic material behaviour of concrete, which may help with the dimensioning of experiments as well as with the interpretation and, possibly, the extrapolation of the experimental results.
Numerous plausibility test and parameter studies of concrete’s dynamic material behaviour, in particular, shock wave propagation and spall fracture, made out a good part of our work in 2015.
Report in the year book 2014
Discrete element simulations: (dis-)continuum included
Quasicontinuum: A virtual specimen, prepared for compressive or tensile loading. Strong cohesive interaction forces between adjacent particles cause form stability and strength.

Discontinuum: The same virtual specimen as before, after all cohesive interaction force have been set to zero. The specimen loses stability and behaves like granular
The design of buildings in massive construction requires a great number of complex static and dynamic computations. In order to manage the computational effort, sophisticated, tried-and-tested computer programs are used. These programs usually implement continuum-based models to describe the material behaviour, i. e. models which assume that the laws of continuum mechanics apply to the material’s behaviour and failure mechanisms.
Concrete and reinforced concrete are especially challenging materials with respect to such continuum-based approaches. Not only is concrete an extremely heterogeneous material by itself, but in most applications concrete needs to be reinforced because of its tendency to crack under tensile stress. Cracks, on the other hand, cannot easily be simulated by continuum-based models of material behaviour, since on principle, they have to be treated as discontinuities. Additional theoretical considerations and programming efforts are necessary to provide those models with more or less realistic damage behaviour, which primarily, will only be able to replicate the experimental results that are used for calibration.
The aim of this research project is to perform numerical experiments by means of 3-dimensional discrete element simulations in order not only to replicate, but even to explore and to observe concrete’s and reinforced concrete’s material behaviour and failure mechanisms. DEM simulations (also: many-body simulations, particle simulations) avoid to take the long way round through continuum mechanics and deal in a straightforward manner with spatially discretized structures and substructures. Cracks, i. e. discontinuities, are in this context not to be considered as a feature added to the model, they simply emerge when particles, formerly connected by cohesive interaction forces, happen to be separated by external tensile forces and shear stress. In this sense, discontinuity is included in the computational approach. If, on the other hand, the material shows no tendency to crack and fail, this is also consistent with the approach used. Continuous material behaviour is a proper subset of the primarily much more complicated material behaviour due to failure, fracture, discontinuities: (dis-)continuum included.
The aspect of numerical stability as well as the correlation of the simulation results with real-world experiments in quality and quantity made out a good part of our work in 2014.
Report in the year book 2013
On Running Dominoes and Reinforced Concrete
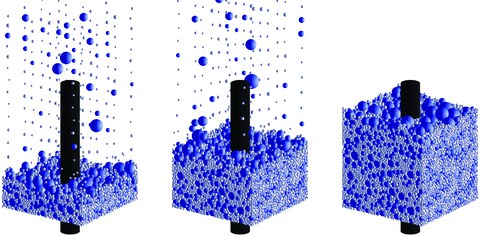
Fill virtual aggregate material around a simple reinforcement bar.
The process of filling a container with granular matter, the formation of a stellar system and the formation of a galaxy, the spreading of a rumor, and the emergence of a traffic jam have at least one thing in common: They show that a complex system‘s behavior emerges from interaction of a great number of particles, objects, or human beings. The image of running dominoes may be the most impressive visual representation of the principle of causality generating complexity that governs nature and our daily life.
Many-body simulations adopt this principle in an idealized manner. Based on a simple (but not too simple) constitutive law for particle-particle interaction, the particles are given respective initial conditions, before the system is left to its own. The constitutive law and its parameters are the only assumptions made in advance of the simulations, so all other phenomena are to be considered as simulation results. This is the fundamental difference between many-body simulations (in particular: the Method of Discrete Elements, DEM) and continuum-based methods such as the Method of Finite Elements (FEM).
In the course of this research project many-body simulations of multiaxial damage behavior of concrete are to be developed which may allow to observe and even explore material behavior and damage processes. The virtual specimens used for the simulations are generated as dense packings of spherical aggregates having size distributions that are oriented towards realistic sieving lines of concrete.
Each individual specimen may be used for numerous situations of loading, may they be uniaxial or multiaxial, monotonic or cyclic, possibly for situations that cannot be realized in the laboratory for principle or practical reasons. Slight modifications of the size distribution of the virtual aggregates and even the generation of different virtual specimens consisting of an identical ensemble of aggregates (so-called „clones”) are possible and allow to repeat the numerical experiments under slightly different initial conditions any number of times.
Report in the year book 2012
Even More Experiments – on the Computer Screen
Crack propagation in a virtual specimen loaded in compression with a view through one of the loading platens.
Simulating uniaxial and multiaxial failure mechanisms of concrete by pairwise interaction of a large number of particles is the purpose of this research project. The model to be developed is intended to show substantial phenomena of concrete‘s failure and post-failure behavior in qualitative and semi-quantitative manner when loaded in compression or tension. The results of the laboratory experiments are the guideline for what we are trying to do in numerical experiments.
As is the case in the lab, virtual specimens are generated as a dense packing of particles representing aggregates, having sizes that are oriented towards realistic sieving lines of concrete. As is the case in the lab, a phase follows in which the particles are pasted, which is achieved by successively leading the contact model from the repulsive to the cohesive regime. As is the case in the lab, this lets the specimen lose a little of its volume, thereafter being prepared for uniaxial or multiaxial loading tests.
In difference to the lab, virtual specimens, once they are created, are available for any number of numerical experiments, e.g. for experiments with various combinations of compressive and/or tensile stress, with or without restraint of lateral strain near the loading plates, with varying loading rates or monotonous or cyclic loading regimes.
While developing the simulation we consider phenomena such as relaxation or effects of inertia at higher strain rates not to be features or add-ons to the model, we believe that they and other phenomena are inherent to the approach chosen.
It might appear a fascinating idea to make happen on a computer screen what happens in the laboratory. Numerical simulations, however, cannot even try to copy reality, and they are not meant to do so. An algorithm which could exactly replicate the real world would be rather useless, since the most powerful „computer“ is nature by itself. The value of numerical simulations lies in finding models, in simplification and abstraction and in the better understanding of the things around us. Having this in mind, we hope that our research project can help with a better understanding of concrete and its mechanisms of damage.
