DEM-Simulation der mehraxialen Schädigungsverhaltens
Inhaltsverzeichnis
Projektdaten
|
Titel | Title |
Bericht im Jahrbuch 2019
DISKRETE-ELEMENTE-SIMULATION DES BETONMATERIALVERHALTENS IN 3D

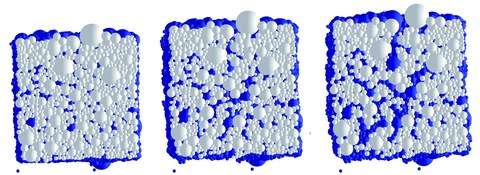
Virtueller Betonprobekörper – Partikelensemble mit verschiedenen Kugeldurchmessern
Im Rahmen dieses Forschungsprojektes wird das Material- und Schädigungsverhalten von Beton mit der Diskrete Elemente Methode (DEM) untersucht. Hierfür wird in diesem Projekt eine Simulation mit sphärischen – d. h. kugelförmigen – Partikeln verwendet. Kugelpartikel haben den enormen Vorteil, dass allein durch Kenntnis des Partikelmittelpunkts und des Radius‘ das Partikel vollständig beschrieben ist. Außerdem vereinfacht es die Kontaktdetektion erheblich. Die Überprüfung, ob zwei benachbarte Partikel sich tatsächlich berühren bzw. überschneiden und auf diese Weise eine rückstoßende Kraft übertragen, ist für sphärische, kugelförmige Partikel mit weitaus geringerem Rechenaufwand zu führen als mit polygonal berandeten Partikeln. Allerdings haben sphärische Partikel den polygonalen Partikeln gegenüber den Nachteil, dass sie keinen Formschluss erlauben und immer zwingend eine zusätzliche kohäsive Bindekraft benötigen, um als Ensemble zusammenzuhalten. In der Simulation sind sowohl Partikelkonfigurationen mit verschiedenen Partikelradien als auch mit gleichen Partikelradien untersucht worden.
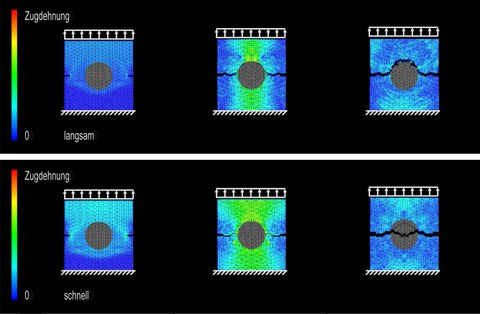
Numerische Simulationen zum mehraxialen Schädigungsverhalten von Beton mit Hilfe der Methode der Diskreten Elemente
Ein virtueller Probekörper wird generiert, in dem eine gewünschte Anzahl von Kugeln verschiedener Größe durchmischt und geschüttet werden, so dass sich als Ergebnis des Preprocessings der generierte Betonprobekörper ergibt. Die verwendeten Partikelradien orientieren sich dabei an einer realen Sieblinie des Betons, repräsentieren also Zuschlag- bzw. Gesteinskörner unterschiedlicher Größe. Werden demgegenüber alle Partikel in derselben Größe generiert, ergibt sich hieraus stets eine hexagonale Partikelanordnung als dichteste Packung. Diese Vereinfachung im Partikelmodell reduziert den Rechenaufwand erheblich. Mit dieser vereinfachten Modellvariante wurden Simulationsrechnungen mit einaxialer Zugbeanspruchung unter verschiedenen Belastungsgeschwindigkeiten durchgeführt und die Rissentstehung und das Risswachstum untersucht. Bei den Untersuchungen stand besonders im Fokus, ob sich ein Riss um ein in einer Zementmatrix befindliches einzelnes Zuschlagkorn herum fortsetzt oder durch das Zuschlagkorn hindurch, ob also das Zuschlagkorn infolge der Belastung bestehen bleibt oder zerbricht. Die Simulation zeigt, dass sich bei geringerer Belastungsgeschwindigkeit der Riss um das Zuschlag- bzw. Gesteinskorn herum fortpflanzt, wohingegen der Riss bei hoher Belastungsgeschwindigkeit durch das Zuschlagkorn hindurchgeht und das Zuschlagkorn zerbricht.
Bericht im Jahrbuch 2018
DEM - KONTINUIERLICH DISKONTINUIERLICH

Festbetonprobekörper nach dem Spallationsversuch am Hopkinson-Bar
Die uns umgebende Welt ist diskontinuierlich, voller Lücken und diskret, das Kontinuum nur eine – allerdings sehr praktische – Vereinfachung. Dabei erfordert diese Vereinfachung einen umfangreichen mathematischen Apparat und einen enormen Sachverstand, um auch nur einfachste Geometrien und Materialannahmen numerisch abbilden zu können. Vielfach, nein: in aller Regel ist man am Ende doch wieder darauf angewiesen, Raum und Zeit zu diskretisieren und dem Computer die Lösung der Gleichungen zu überlassen.
Die Methode der diskreten Elemente (DEM) gehört zur Kategorie der partikelbasierten Methoden. Sie vermeidet den „Umweg“ über die Kontinuumsmechanik und arbeitet direkt mit den der Teilchen-Teilchen-Wechselwirkung zugrundeliegenden Phänomenen. Die Newtonschen Bewegungsgleichungen bilden dabei gleichsam das Fundament, auf dem und um das herum geeignete Bausteine zur Beschreibung von Formschluss, Kohäsion und Reibung angeordnet werden. Kinematik und Dynamik sind hier keine hinzuzufügenden „Features“, sondern inhärenter Teil der Methode.

Virtueller Betonprobekörper für den numerischen Spallationsversuch
Im Spallationsversuch – der kurzen, schockartigen Belastung eines Festkörpers mit bekannten statischen Materialeigenschaften durch einen Impaktor oder ein Projektil – treffen die verschiedenen Welten aufeinander: die körnige und die kontinuierliche, die statische und die dynamische. Er stellt eine Schnittstelle dar zwischen der diskreten mesoskopischen Ebene von Zementmatrix und Zuschlagkorn und der makroskopischen Welt, in der wir leben und bauen. Gleichzeitig ist er ein ausgezeichnetes Versuchsfeld zum Studium unterschiedlicher numerischer Methoden.
Der virtuelle Spallationsversuch war einer der Schwerpunkte dieses von der Deutschen Forschungsgemeinschaft geförderten Projekts. Die einzelnen Schritte der Simulation bestehen dabei zunächst in der Generierung des virtuellen Probekörpers („Mischen“ und „Aushärten“) und der Modellierung der anderen am virtuellen Experiment beteiligten Objekte. Anschließend werden der Simulationsraum konfiguriert und die Objekte darin positioniert und initialisiert („Einspannen“, „Laden“). Wie im Labor versetzt man sich daraufhin in die Rolle des Beobachters und verzeichnet die im Simulationsraum sich ergebenden Phänomene („Messen“). Auf diese Weise hoffen wir, das Laborexperiment besser verstehen zu können, Nicht-Sichtbares sichtbar zu machen und weitere reale oder virtuelle Experimente besser planen zu können.
Bericht im Jahrbuch 2017
EIN EFFEKT, DER KEINER SEIN SOLL – UND DER MANN MIT DEN ZWEI UHREN

Zuschlagkorn in Mörtelmatrix – Zugversuch bei moderater Belastungsgeschwindigkeit: Risswachstum von der Kerbe hin zum Korn …
Postuliert, experimentell bestätigt, dann wieder zum bloßen Mythos erklärt – der sogenannte Dehnrateneffekt ist Streitthema sowohl unter Theoretikern als auch unter praktisch tätigen Ingenieuren. Gemeint ist die vermeintliche oder tatsächliche Festigkeitssteigerung von Beton bei hohen Belastungsgeschwin-digkeiten, wie sie in Anprall- und Impaktsituationen auftreten.
Strittig sind dabei weniger die jeweiligen Versuchsanordnungen und Messergebnisse als vielmehr deren Interpretation und Zuordnung zu verschiedenen Erklärungsmustern. So stellen einige Forscher den Effekt – weil angeblich einzig auf Trägheitseffekten beruhend – gänzlich in Frage. Andere erkennen zumindest einen Teil des Effektes als materiell an. Eine der gängigsten Erklärungen sieht im Zerbrechen des Zuschlagmaterials bei höheren Dehnraten einen wesentlichen Faktor zur Beschreibung des Phänomens.
Impaktsituationen zeichnen sich durch extreme Kurzzeitigkeit aus, was frühere Experimente zum dynamischen Materialverhalten sehr schwierig gestaltete. Inzwischen stehen mit Dehnmessstreifen auf Halbleiterbasis und Piezo- Beschleunigungs-aufnehmern geeignete Instrumente zur zeitlichen Auflösung der das Material durchlaufenden Stoßwellen zur Verfügung. Allerdings stellt diese Auflösung den Experimentator vor ein neues Problem: Da die Messtechnik an verschiedenen Stellen des Probekörpers appliziert wird, die Wellenausbreitungsgeschwindigkeit im Material aber begrenzt ist, misst die Technik nun doppelt und dreifach, was früher nur gemittelt über größere Bereiche erfasst werden konnte. In gewisser Weise geht es dem Forscher also wie dem Mann mit den zwei Uhren – er kennt zwei Uhrzeiten, aber welche ist die richtige?
Numerische Simulationen können helfen, die vielfältigen Effekte von Wellenausbreitung, Reflexion und Schädigung im Material sichtbar und damit verständlicher zu machen. Sie sollen das Laborexperiment nicht ersetzen, sondern sinnvoll ergänzen und bei der Interpretation der experimentellen Ergebnisse von Nutzen sein. Die Methode der diskreten Elemente (DEM) scheint besonders geeignet, Effekte wie Stoßwellenaus-breitung und Schädigung im numerischen Experiment zu untersuchen. Da sie fast völlig auf den Newton‘schen Bewegungsgleichungen beruht, sind Trägheitseffekte integraler Bestandteil der Simulationsergebnisse – und können entsprechend qualifiziert, quantifiziert oder auch ganz herausgerechnet werden.
Bericht im Jahrbuch 2016
DEM-Simulation von Ausziehversuchen

Modellierung eines virtuellen dynamischen Ausziehversuchs mit ca. 9.000 Teilchen vor dem Ausziehversuch (Ruhelage) und zu Beginn des Ausziehversuchs, d. h. kurz nachdem der Bewehrungsstab schlagartig beschleunigt wurde. Blau = ruhende Partikel, rot = Partikel mit hoher Geschwindigkeit
Stahlbeton – der Begriff verrät es bereits – ist nur dann richtig tragfähig, wenn Beton und Stahl zusammenwirken und wenn ein Verbund beider Komponenten gewährleistet ist. Um den Verbund beziehungsweise die Verankerung des Bewehrungsstahls im Beton zu untersuchen, werden sogenannte Ausziehversuche in Laborexperimenten durchgeführt.
Für Parameterstudien ist es zweckmäßig, solche Ausziehversuche auch in der numerischen Simulation abzubilden. In dem Forschungsprojekt zur Diskrete-Elemente-Simulation wird u. a. die Verbundwirkung von Stahl und Beton bei numerischen Ausziehversuchen an würfelförmigen und zylindrischen virtuellen Probekörpern untersucht. Dabei geht es weniger darum, die geometrischen Verhältnisse realer Bewehrungsstäbe nachzubilden, sondern darum, in Tastversuchen das Potential der Methode bei der Simulation von Ausziehversuchen zu erkunden. Die Simulationsrechnungen werden für Auszieh-/Pull-out-Versuche unter quasistatischen und dynamischen Bedingungen durchgeführt. Hierfür wird der 3D-Simulationscode mit gleich großen kugelförmigen und daher hexagonal dicht gepackten Teilchen verwendet.
In der Simulation wird der Probekörper durch ein Ensemble von Partikeln repräsentiert. Die Kräfte werden dabei durch benachbarte, sich kontaktierende Partikel wechselseitig übertragen. Für die Partikel des Betonkörpers und des Bewehrungsstahls werden jeweils unterschiedliche Materialparameter verwendet. Der Verbund von Beton und Bewehrungsstab wird durch eine Mischungsregel (hier: die Lorentz-Berthelot-Mischungsregel) für die Verbundzone und vor allem durch die geometrische Verzahnung der Rippen des Bewehrungsstabes im Betonmaterial modelliert. Mit Hilfe der Simulation kann die Wellenausbreitung im virtuellen Probekörper sichtbar gemacht werden. Deutlich zu sehen sind die typischen, von den Rippen des Bewehrungsstabes ausgehenden, nach vorn gerichteten Stoßwellenkegel, die sich im umgebenden Betonmaterial ausbreiten. Bei der Simulation von Ausziehversuchen wird ein großes Potential der Diskrete-Elemente-Methode insbesondere darin gesehen, dass die in der geometrischen Verzahnung stattfindende Kraftübertragung modelliert werden kann und dass die Simulation die auch im Laborexperiment beobachteten Risse und Hohlräume auf der Rückseite der Bewehrungsrippen abbildet.
Bericht im Jahrbuch 2015
Beton ist grau und undurchsichtig?
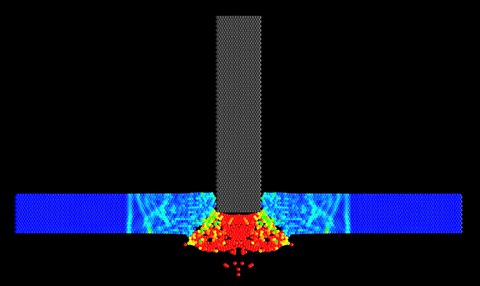
Impaktsimulation: Durchstanzen einer Platte; deutlich sind Durchstanzkegel und Stoßwellenausbreitung im virtuellen Probekörper zu sehen
Beton besitzt neben seinen bekannten statischen Materialeigenschaften, die ihn zum mit großem Abstand meistgenutzten Werkstoff für Massivbaukonstruktionen machen, eine Vielzahl dynamischer Eigenschaften, die sowohl von theoretischem als auch von zunehmend praktischem Interesse sind – man denke etwa an die verheerende Wirkung von Erdbeben, den Anprall großer, sich bewegender Massen oder die Problematik des Einschlags von Objekten mit hoher kinetischer Energie.
Impaktsituationen zeichnen sich durch ihre extreme Kurzzeitigkeit aus, die einerseits aus der Plötzlichkeit der Einwirkung, andererseits aus der sehr hohen Ausbreitungsgeschwindigkeit der durch die Einwirkung im Material erzeugten Stoßwellen resultieren. Diese Kurzzeitigkeit stellt das Laborexperiment vor nicht unerhebliche Probleme. Zum einen müssen entsprechende Impaktsituationen mit maschinellem Aufwand generiert werden. Falltürme, Beschussanlagen oder der Split-Hopkinson-Bar sind komplexe ingenieurtechnische Vorrichtungen, die mit hohem Aufwand entworfen, betrieben und gewartet werden müssen. Darüber hinaus lassen sich die durch die applizierte Messtechnik gewonnenen experimentellen Daten nicht immer und nicht ohne weiteres sofort und richtig interpretieren, da das getestete Material nicht durchsichtig ist.
Numerische Simulationen verfolgen die Absicht, das Material ein wenig „durchsichtiger“ zu machen. Sie erlauben es, eine zumindest qualitative Vorstellung davon zu gewinnen, welche Phänomene hinsichtlich Stoßwellenausbreitung und Schädigung zu erwarten und im jeweiligen Probekörper wo und wann messbar sind. Diskrete-Elemente-Simulationen haben darüber hinaus das Ziel, das Material Beton nicht als Kontinuum zu behandeln, zu begreifen und zu beschreiben. Risse, Abplatzungen und die Ausstoßung ganzer Kegel von virtuellem Material stellen keine hinzuzufügenden Features dar, sie sind Bestandteil der Rechnung. Aktuell wird im Rahmen dieses Forschungsprojektes daran gearbeitet, gerade auch das dynamische Materialverhalten von Beton im numerischen Experiment nicht nur abbilden, sondern sein Schädigungsverhalten gleichsam entdecken und beobachten zu können.
In diesem Jahr standen zahlreiche Plausibilitätstests und umfangreiche Parameterstudien zum dynamischen Materialverhalten von Beton, insbesondere zu Schockwellenausbreitung und Spallation im Mittelpunkt.
Bericht im Jahrbuch 2014
Diskrete-Elemente-Simulationen: (Dis-)Kontinuum inbegriffen
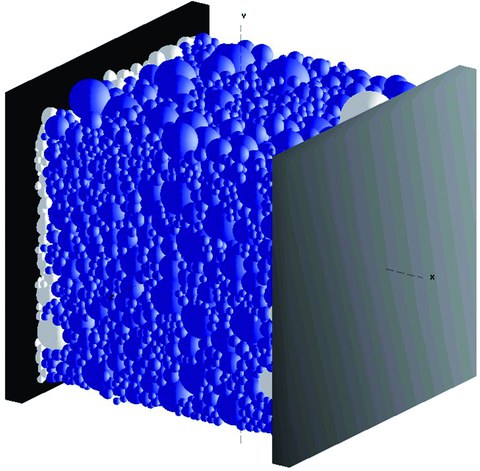
Quasikontinuum“: Ein virtueller Probekörper, vorbereitet für den einaxialen Druck- oder Zugversuch. Starke kohäsive Verbindungen zwischen benachbarten Zuschlagkörnern sorgen für Formstabilität und Festigkeit.

Diskontinuum: Derselbe Probekörper nach dem Lösen aller kohäsiven Verbindungen. Das virtuelle Zuschlagmaterial verliert jegliche Formstabilität und verhält sich stattdessen wie Schüttgut.
Komplexe statische und dynamische Berechnungen bilden mittlerweile einen unverzichtbaren Bestandteil beim Entwurf von Massivbaukonstruktionen. Dabei kommen erprobte, leistungsfähige Computerprogramme zum Einsatz, in denen in der Regel kontinuumsbasierte Materialmodelle implementiert sind, also Materialmodelle, die dem Material zunächst die Gültigkeit der Gesetze der Kontinuumsmechanik unterstellen.
Das Material (Stahl-)Beton stellt diese Programme vor besondere Herausforderungen. Nicht nur handelt es sich bei der Komponente Beton um einen hochgradig heterogenen Baustoff. In den allermeisten Fällen ist es auch nötig, ihn zu bewehren, denn er neigt bereits im Zustand der Gebrauchstauglichkeit zur Rissbildung. Risse − oder eben: Diskontinuitäten − aber widersprechen den genannten kontinuumsbasierten Ansätzen und müssen in geeigneter Weise in diese eingearbeitet oder ihnen hinzugefügt werden. Hierbei kommen zum Beispiel spezielle Kontakt- oder Risselemente zur Anwendung, deren Wirkungsmechanismen in aufwändiger Weise durch theoretische Überlegungen und experimentelle Ergebnisse gewonnen werden müssen, und die ihrem Wesen nach das Materialverhalten „nur“ abbilden können.
Im Rahmen dieses Forschungsprojektes wird versucht, das Materialverhalten von Beton im numerischen Experiment nicht nur abbilden zu können, sondern sein Schädigungsverhalten gleichsam entdecken und beobachten zu können. Diskrete-Elemente-Simulationen (auch: Mehrkörpersimulationen, Vielteilchensimulationen oder Partikelsimulationen) verzichten auf den Umweg über das meist ohnehin nicht vorhandene Kontinuum und basieren unmittelbar auf räumlich diskretisierten Strukturen. Risse, also Diskontinuitäten, stellen dabei kein hinzuzufügendes Feature dar, sondern äußern sich einfach durch die stoffliche Trennung vormals miteinander verbundener Teilchen – das Diskontinuum ist im Modell also inbegriffen. Sollte das Material sich allerdings dazu entschließen, nicht zu versagen, so ist auch dies im Modell enthalten. Kontinuierliches Materialverhalten ist eine echte Teilmenge des in der Regel komplizierteren Materialverhaltens: (Dis-)Kontinuum inbegriffen.
In diesem Jahr standen insbesondere Aspekte der numerischen Qualität sowie der qualitativen und quantitativen Vergleichbarkeit von Experiment und Simulationsergebnissen im Mittelpunkt.
Bericht im Jahrbuch 2013
Viele Teilchen: Dominos und Stahlbeton
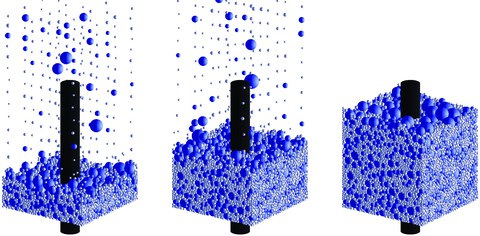
Schüttung des virtuellen Zuschlagmaterials um einen einfachen Bewehrungsstab.
Die Befüllung eines Silos mit Schüttgut und die Ausbildung von Kugelsternhaufen oder ganzer Galaxien, die Ausbreitung von Gerüchten und die Entstehung von Verkehrsstaus zeigen eine Gemeinsamkeit: Systemverhalten entsteht durch die Interaktion einer Vielzahl von Teilchen, Objekten oder Personen. Die Ansicht einer Kette fallender Dominosteine ist das vielleicht eindrücklichste Sinnbild des für die Natur grundlegenden Prinzips von einfacher Ursache und komplexer Wirkung.
Vielteilchensimulationen folgen diesem Prinzip, indem sie es nachbilden. Ausgehend von einem möglichst einfachen Modell für die Teilchen-Teilchen-Interaktion wird das System in einen bestimmten Anfangszustand gebracht und anschließend sich selbst überlassen. Das verwendete Kontaktmodell und die darin auftretenden Parameter sind die einzigen Annahmen, die im Vorfeld der Simulationen zu treffen sind, alle nachfolgend beobachteten Phänomene und Effekte hingegen stellen die Ergebnisse der Simulation dar. Dies unterscheidet Vielteilchensimulationen (speziell: die Methode der Diskreten Elemente, DEM) grundlegend von kontinuumsbasierten Methoden wie etwa der FEM.
In diesem Projekt werden Vielteilchensimulationen des mehraxialen Schädigungsverhaltens von Beton entwickelt, mit denen sich das Materialverhalten und die Schädigungsmechanismen gleichsam beobachten und entdecken lassen. Die verwendeten virtuellen Probekörper werden als Schüttung kugelförmiger Zuschlagteilchen erzeugt, welche sich in ihrer Größe an realistischen Sieblinien orientieren. Der Simulationscode erlaubt die Generierung unterschiedlichster Probekörpergeometrien ebenso wie die Schüttung des virtuellen Zuschlagmaterials um einfache Arten der Bewehrung herum. In der nachfolgend simulierten Phase des Aushärtens sorgt eine geeignete Modifikation des Kontaktmodells dafür, die erhaltenen Haufwerke zu formstabilen Probekörpern zu verkleben, die dann für virtuelle Belastungsversuche zur Verfügung stehen.
Jeder einzelne der virtuellen Probekörper kann wieder und wieder unterschiedlichsten Belastungssituationen ausgesetzt werden, ein- oder mehraxial, unter monotoner oder zyklischer Beanspruchung, möglicherweise unter Bedingungen, die im Laborexperiment nur äußerst schwer oder gar nicht zu realisieren sind. Geringfügige Änderungen des virtuellen Zuschlagmaterials, ja sogar die Generierung verschiedener Probekörper aus identischem Zuschlagmaterial, erlauben es, die numerischen Experimente unter leicht veränderten Anfangsbedingungen beliebig oft zu wiederholen.
Bericht im Jahrbuch 2012
Alles fast wie im Labor – virtuelle Probekörper
Rissentwicklung im einaxialen Druckversuch mit Blick durch eine der Belastungsplatten hindurch
Im Rahmen dieses Forschungsvorhabens wird der Versuch unternommen, das Schädigungsverhalten von Beton unter ein- oder mehraxialer Belastung durch die paarweise Interaktion einer Vielzahl von Teilchen zu simulieren. Das zu entwickelnde Modell soll in der Lage sein, wesentliche Aspekte des Bruch- und des Nachbruchverhaltens von Beton in qualitativer bis halbquantitativer Weise nachzuvollziehen. Die Güte der hierbei erhaltenen Ergebnisse muss sich an den Resultaten der Laborexperimente messen lassen.
Fast wie im Labor beginnt die Simulation mit der Generierung eines virtuellen Probekörpers als Haufwerk von Zuschlagkörnern, dessen Korngrößenverteilung sich an einer realistischen Sieblinie für Beton orientiert. Fast wie im Labor folgt eine Phase des „Aushärtens“, wozu das verwendete Kontaktmodell allmählich aus einem anfangs ausschließlich abstoßenden ins abstoßend/anziehende, kohäsive Regime gefahren wird. Und fast wie im Labor verliert der virtuelle Probekörper hierbei ein wenig an Volumen, um anschließend – fest verleimt und formstabil – für ein- oder mehraxiale Belastungsversuche zur Verfügung zu stehen.
Anders als im Labor steht ein und derselbe einmal generierte Probekörper für beliebig viele Belastungsversuche zur Verfügung, für Belastungsversuche mit verschiedenen mehraxialen Belastungskombinationen ebenso wie für Versuche mit unterschiedlichen Belastungsgeschwindigkeiten, bei behinderter oder unbehinderter Querdehnung, geradewegs bis zum Versagen oder aber unter zyklischer Beanspruchung.
Die in Entwicklung befindliche Simulation versteht Phänomene wie etwa Relaxation oder Verfestigungs- sowie Trägheitseffekte bei höheren Dehnungsraten nicht als hinzuzufügende Funktionalitäten, vielmehr werden diese und andere Erscheinungen als dem Modell innewohnend angenommen.
Die Prüfmaschine im Rechner – das ist eine verlockende Vorstellung. Numerische Simulationen jedoch können und sollen keine Kopien der Wirklichkeit liefern. Ein die Natur exakt nachbildender Algorithmus wäre vollkommen nutzlos, denn den leistungsfähigsten „Rechner“ stellt die Natur selbst dar. Der Nutzen numerischer Simulationen besteht in der Modellbildung, der Vereinfachung und Abstraktion, im besseren Verständnis der uns umgebenden Dinge. In diesem Sinne hoffen wir, mit diesem Forschungsvorhaben zu einem besseren Verständnis des Materials Beton und seiner Schädigungsmechanismen beitragen zu können.
