Beschreibung
Stichworte:
nicht ebene Grundwasserströmung, freie Randwertprobleme, analytische Lösung, Fluss-Grundwasser-Austausch
Zielstellung
Die von Schmitz und Edenhofer [1, 2] gefundene analytische Lösung der 2D-Laplacegleichung für die stationäre nicht ebene Grundwasserströmung im tiefen, homogenen und isotropen Aquifer soll verallgemeinert und für hydrologische Anwendungsfälle erschlossen werden. Im Vordergrund stehen:
- die Einbeziehung von inneren Quellen/Senken (Poissongleichung)
- die Betrachtung seichter Aquifere
- die Berücksichtigung fester seitlicher Ränder
- die Herleitung von Formeln für das inverse Problem, aus einem vorgegebenen Grundwasserspiegel die Zusickerungs-/Entnahmerate zu ermitteln
- die semi-analytische Lösung des instationären Problems
- die Betrachtung geometrisch beliebiger unterer Ränder
Die hergeleitete Lösung soll sowohl im Softwarepaket TEXAS2D als auch in Form eines Softwaremodules verfügbar gemacht werden, das sich mit anderen Grundwassermodellen koppeln lässt.
Neben der Erweiterung der mathematischen Lösung erfolgt deren hydrologisch-ingenieurwissenschaftliche Erschließung und Interpretation:
- Anwendung der inversen Rechnung zur Bestimmung der Austauschwassermenge zwischen Oberflächengewässer und Grundwasserleiter
- Sensitivitätsanalyse, Vergleich mit herkömmlichen Modellen, Labor- und Felddaten
- Integration der mathematischen Lösung in einem anwenderorientierten hydrodynamisch-analytischen Softwaretool
Methoden
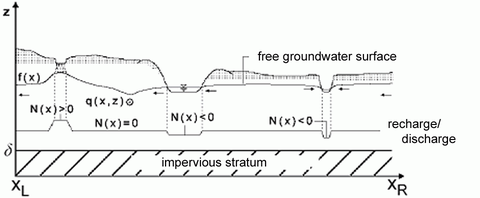
Betrachtet wird ein homogener isotroper Aquifer mit freier Oberfläche und undurchlässiger, horizontaler unterer Berandung. Die Zusickerung / Entnahme von Grundwasser wird durch eine Funktion N(x) oder innere Punktquellen bzw. -senken beschrieben.
Das Grundprinzip der analytischen Lösung besteht in der konformen Transformation des Aquifers mit freiem oberen Rand auf einen Parallelstreifen. Das transformierte Randwertproblem wird auf dem Parallelstreifen gelöst. Die Kenntnis der freien Grundwasseroberfläche erlaubt dann die Rücktransformation der Lösung.
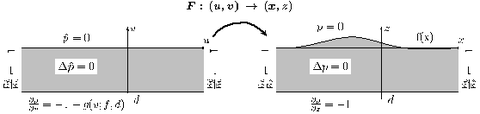
Lösung des Randwertproblems mit Parallelstreifen
Der entscheidende Schlüssel, sowohl zur Lösung des direkten stationären als auch des inversen Problems ist die Herleitung einer Beziehung zwischen der Zusickerung / Entnahme N und der Grundwasseroberfläche f im transformierten Gebiet. Dieselbe Gleichung erlaubt eine semi-analytische Lösung des instationären Problems, indem die zeitliche Änderung der Grundwasseroberfläche in jedem Zeitschritt analytisch ermittelt wird, während die Aktualisierung der Grundwasseroberfläche numerisch erfolgt.
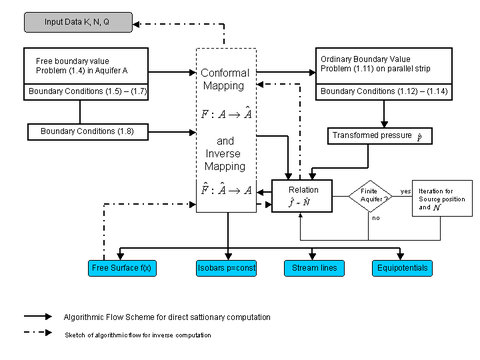
Lösung des instationären Prozesses
Seitliche Begrenzungen des Beobachtungsgebietes werden durch geeignete Anordnungen von Quellen bzw. Senken definiert. Details zum mathematischen Algorithmus und dessen Umsetzung im Softwareprogramm TEXAS2D enthält das zugehörige Manual. Ausführlich Informationen zu den theoretischen Herleitungen finden sich in der Dissertation von J. Weber, TU München.
Die inverse Rechnung eröffnet völlig neue Möglichkeiten zur Bestimmung von Austauschwassermengen zwischen Grundwasserleiter und Oberflächengewässer. (genauer)
Ergebnisse
Die Lösung des stationären direkten und inversen Grundwasserproblems sind bereits im Software-Tool (Tool for EXact Analytic Solution of 2D-groundwater flow problems) implementiert. Die instationäre Lösung und die inverse Berechnung für seichte Aquifere werden gegenwärtig erprobt.