Promotionsprojekt 6: Konstitutive Modellierung, mehrskalige und multiphysikalische Simulation der I-FEV
Inhaltsverzeichnis
Motivation
I-FEV bestehen üblicherweise aus Elastomermatrix, integriertem aktivem Material (z.B. dielektrischer Elastomer-Aktor) und eingebetteten Faserverstärkungen. Die Funktionalität von I-FEV beruht hauptsächlich auf der Interaktion zwischen der Matrix, der externen Anregung und der mechanischen Antwort des integrierten aktiven Materials. Abhängig vom aktiven Material, das in dem Verbund Anwendung findet, basiert die Anregung auf dem induzierten thermischen, elektrischen und magnetischen Feld. Die Vorhersage der Antwort dieses hochgradig heterogenen Materials unter Berücksichtigung der Interaktion der genannten Felder erfordert eine adäquate mathematische Umsetzung des konstitutiven Verhaltens und rechentechnisch effiziente Simulationsansätze.
| Fischflossen-ähnliche Struktur | Heterogenes elektro-aktives Material |
Stand der Forschung und eigene Vorarbeiten
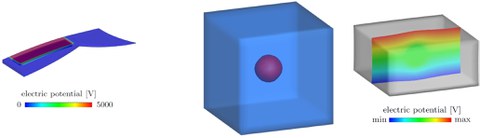
Die numerische Modellierung des multiphysikalischen Verhaltens der Strukturkomponenten baut auf einem bereits entwickelten thermo-elektro-mechanischen konstitutiven Modell und einer entsprechenden Finite Elemente Umgebung (1. Kohorte) auf, in der die verschiedenen multiphysikalischen Kopplungen zwischen den thermischen, mechanischen und elektrischen Feldern berücksichtigt sind [1-4] (siehe Abbildung). Die Beschreibung des imperfekten Verbunds zwischen den verschiedenen Komponenten und der zugehörigen Delamination basiert auf einem thermo-mechanischen Interface-Element. Der numerischen Struktursimulation der Komposite liegt eine multiphysikalische Homogenisierung zugrunde, die die effektiven Materialeigenschaften und den Übergang zwischen den verschiedenen Längenskalen auf effiziente Weise liefert (entkoppelte Homogenisierung [5]). Dieser grundlegende Ansatz [5] ist bisher nicht für eine Drei-Feld-Homogenisierung und nicht für die erwähnten Feldgrößen (thermisch, elektrisch, mechanisch) entwickelt. Die Aufgabe der 2. Kohorte ist es, diese Forschungslücke zu schließen.
Wissenschaftliche Fragestellung und Projektziele
Ein Ziel dieses PP 6 ist die Entwicklung eines Homogenisierungsansatzes für thermo-elektro-mechanische Feldgrößen. Der mehrskalige und multiphysikalische Übergang zwischen den Längenskalen für das Dreifeldproblem erfordert rechentechnisch effiziente Methoden. Ein bereits existierender (über die Längenskalen) entkoppelter (thermo-mechanisch voll gekoppelter) Zweifeldansatz wird um das dritte (elektrische bzw. magnetische) Feld erweitert. Die Evolution der Schädigung im Interface zwischen der Matrix und der Verstärkung wird über eine adäquate Interfaceformulierung berücksichtigt. Zunächst wird dazu ein makroskopisches Materialmodell entwickelt, das die vollständig gekoppelte Materialantwort und die effektiven Eigenschaften adäquat, einschließlich aller relevanten physikalischen Phänomene, beschreiben kann. Weiterhin werden Randbedingungen für ein zu definierendes repräsentatives Volumenelement (RVE) zur Homogenisierung der heterogenen Charakteristiken entwickelt. Final werden die Eigenschaften des makroskopischen Materialmodells anhand der Homogenisierung des RVE identifiziert, um effektive Struktursimulationen auf einer großen Längenskala zu realisieren. Zusätzlich zum zweiskaligen thermo-elektro-mechanischen Ansatz ist geplant, eine magneto-mechanische Erweiterung der Modelle und Simulationsansätze zu entwickeln.
Literatur
| [1] | A. Kanan, M. Kaliske. Finite element modeling of electro-viscoelasticity in fiber reinforced electro-active polymers. International Journal for Numerical Methods in Engineering, 122:2005-2037, 2021. |
| [2] | A. Kanan, M. Kaliske. On the computational modelling of nonlinear electro-elasticity in heterogeneous bodies at finite deformations. Mechanics of Soft Materials, 3:1-19, 2021. |
| [3] |
R. Vertechy, G. Berselli, V.P. Castelli, M. Bergamasco. Continuum thermo-electromechanical model for electrostrictive elastomers. Journal of Intelligent Material Systems and Structures, 24:761–778, 2013. |
| [4] |
M. Mehnert, J.-P. Pelteret, P. Steinmann. Numerical modelling of nonlinear thermo-electro-elasticity. Mathematics and Mechanics of Solids, 22:2196-2213, 2017. |
| [5] |
R. Fleischhauer, T. Thomas, J. Kato, K. Terada, M. Kaliske. Finite thermo-elastic decoupled two-scale analysis. International Journal for Numerical Methods in Engineering, 122:355-391, 2020. |
Kontakt
Institut für Statik und Dynamik der Tragwerke (ISD), Fakultät Bauingeneurwesen der TU Dresden
 © Michael Kretzschmar
© Michael Kretzschmar
Institutsdirektor
NameUniv.-Prof. Dr.-Ing. habil. Michael Kaliske
Eine verschlüsselte E-Mail über das SecureMail-Portal versenden (nur für TUD-externe Personen).