Modeling of Aleatoric and Epistemic Uncertainties in the Simulation of Multiphase Steel Structures
The project focusses on the incorporation of aleatoric and epistemic uncertainties in a multi-scale framework for the simulation of micro-heterogeneous materials (e.g. low-alloyed TRIP-steels).
A continuation of the topic is currently taking place in the second project phase.

Optimal bounds on the probability of failure (PoF) of a soft biological tissue under cyclic uniaxial tension taking into account different levels of statistical information. The stretch axis is normalized such that it represents stretches between 4% (f = 0) and 11% (f = 1).
The Projekt aims to reach the following research goals:
- Construction of a computational model for the prediction of macroscopic properties, which directly incorporates the microstructure of the multiphase steel in the sense of FE2. This includes the development of an appropriate material model for the austenitic-martensitic phase transformation in low-alloyed TRIP-steels and a method for the construction of suitable statistically similar RVEs.
- Quantification of microstructural variability, described in terms of suitable morphology descriptors, as e.g. phase fraction, spectral density and lineal-path function, and the analysis of resulting incomplete statistical data regarding macroscopic material properties by computational homogenization.
- Development of a method for the calculation of optimal bounds on the probability of failure of structural components, providing certified statements by only taking into account available statistical information, which avoids assumptions on subjective distribution functions. Comparative analysis will be performed in order to estimate how much statistical data will be at least required to allow for reasonable statements regarding the failure probability of multiphase steel structures.
Summary of the first funding phase
n the first phase of this subproject, three different main goals have been addressed. The first one focused on the development of an extended material model for low-alloyed TRIP steels, which is able to reflect phase transitions in the microstructure as well as the elasto-plastic behavior of the austenite phase. Validations based on computational homogenization of a simple microstructure revealed a good agreement with experimental data.
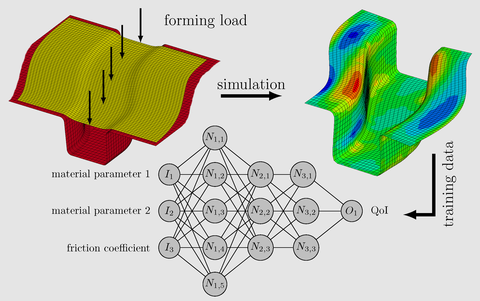
Schematic illustration for the construction of the surrogate model based on a neural network for the considered sheet metal forming process.
Furthermore, a new method for the quantification of uncertain macroscopic material properties due to a variation of the microstructure's morphology was developed, which is based on statistically similar RVEs (SSRVEs). Central element of this new method is the utilization of statistical measures of higher order in a distance functional, which quantifies the inner variation of a real measured microstructure. Based thereon, a set of artificial microstructures is constructed, which exhibits a similar variation of the morphology, but requires a smaller computational effort. In a virtual lab, this set can be tested to compute the corresponding set of homogenized stress-strain-curves, from which the desired macroscopic material properties can be deduced. In the entirety of the set of microstructures, this procedure leads to the distributions of the sought macroscopic properties. In principle, this method is suitable for every type of microstructure, provided that the statistical measures are chosen suitably. In this project, a dual-phase steel was investigated and the variation of macroscopic material parameters related to the hardening behavior was quantified.
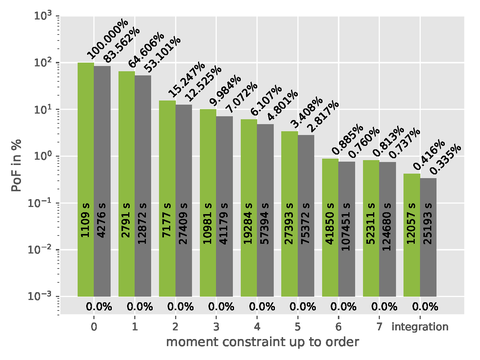
: Optimal, i.e. sharpest, bounds on the PoF for an increasing number of moment constraints on the material parameter k (first 8 × 2 color bars), and bounds on the PoF resulting from an integration of the PDF of material parameter k in the failure region (last 1 × 2 color bars). In addition to that, two different levels of information are considered for the friction coefficient, which is firstly constrained to be within bounds (green color bars, left) and secondly additionally the mean is constrained within bounds (grey color bars). Within the color bars, the required computing is given.
As a third major achievement, the Optimal Uncertainty Quantification (OUQ) framework was extended to polymorphic uncertainties. For this purpose, two different approaches were developed to also include aleatory uncertainties, at which the second approach based on the integration of the joint probability density functions in the failure region, has been identified as the preferable one. This approach is similar to existing approaches known from fuzzy-probability, but in contrast to those methods, the extended OUQ allows to specify not only intervals for uncertain quantities themselves, but also for stochastic moments. Thereby the moment can be a precise value or even an interval. In this partial project the extended OUQ was applied to a sheet metal forming process and both approaches have been compared, which revealed the second approach to be preferred. The numerical simulation of the forming process therein has been replaced by a neural network as surrogate model in collaboration with Steffen Freitag of partial project 6.
Essential project findings
- Materialmodel for low-alloyed TRIP-steel
Mascroscopic uncertainty of material properties - Statistically similar volume elements
- Optimal Uncertainty Quantification for polmorphic uncertainties
- Sheet metal forming processes under polymorphic uncertainties
Prof. Dr.-Ing. habil. Daniel Balzani
Ruhr-Universität Bochum
Lehrstuhl für Kontinuumsmechanik
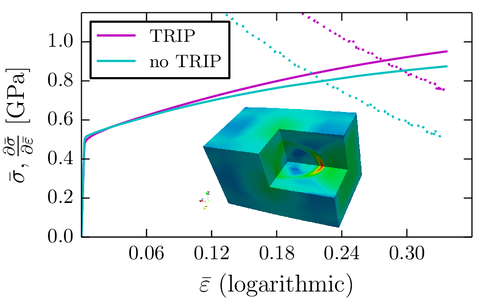
Effect of martensitic phase transformation on macroscopic true stress-true strain curve and local hydrostatic stress distribution for an idealized cubic RVE with a single spherical inclusion undergoing transformation.
In a previous work, optimal uncertainty quantification (OUQ) has been successfully applied to predict optimal bounds on the probability of failure (PoF) of a soft biological tissue under cyclic loading conditions. Sharper bounds on the PoF have been obtained by increasing the levels of available statistical information (Fig.1a). Furthermore, the effect of the martensitic phase transformation in low-alloyed TRIP-steels on the macroscopic properties and on the mesoscopic field distributions has been investigated. It has been confirmed that phase transformation enhances both strength and ductility, but at the same time leads to mesoscopic stress distributions that indicate the initialization of failure at the austenitic martensitic interphase.
- Kremer, K.; Edler, P.; Miska, N.; Leichsenring, F.; Balzani, D.; Freitag, S.; Graf, W.; Kaliske, M.; Meschke, G.
Modeling of structures with polymorphic uncertainties at different length scales.
Surveys for Applied Mathematics and Mechanics (GAMM-Mitteilungen), 2019, Link - Balzani, D., Schmidt, T. and Ortiz, M. (2016) Method for the quantification of rupture probability in soft collagenous tissues. Int. J. Numer. Meth. Biomed. Engng., doi:10.1002/cnm.2781
- Prüger, S., Gandhi, A. and Balzani, D. (2016) Modeling of low-alloyed TRIP-steels based on direct micro-macro simulations. Proceedings: European Congress on Computational Methods in Applied Sciences and Engineering, ECCOMAS 2016, Greece


