Effiziente Bayes'sche Multi-fidelity Verfahren für die Analyse und den Entwurf komplexer gekoppelter Systeme

Das Ziel dieses Projektes ist die Entwicklung eines universellen Werkzeugs für die Unsicherheitsquantifizierung komplexer, realer Multiphysics-Probleme mit hoher stochastischer Dimension, basierend auf neuartigen Bayes'schen Multi-Fidelity-Ansätzen, um eine bislang unerreichte Gesamteffizienz und Genauigkeit zu erzielen. Darüber hinaus ist geplant, das entwickelte Framework zu einem stochastischen Optimierungswerkzeug zu erweitern, mit dem eine robuste Auslegung von Strukturen und Systemen unter Unsicherheit durchgeführt werden kann.

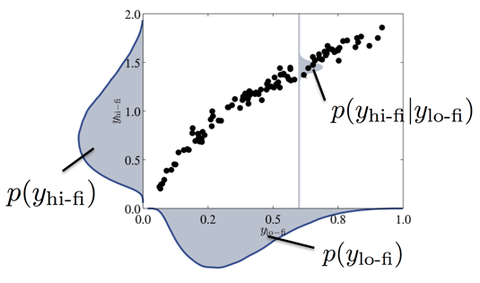
Mit dem entwickelten Satz von UQ-Methoden wird es möglich sein, komplexe, reale Strukturen und Systeme zu untersuchen, die durch hochdimensionale parametrische Unsicherheiten aus der Diskretisierung mehrdimensionaler, nicht-gaußscher Zufallsfelder charakterisiert sind. Die Methoden liefern verlässliche Schätzungen für die Statistik der relevanten Ausgangsgrößen sowie Sensitivitätsmaße für die verschiedenen unsicheren Modelleingangsparameter. Die bisher untragbar hohen Rechenkosten, die mit UQ in solch komplexen und anspruchsvollen Szenarien verbunden sind, werden durch die konsequente Einbindung von Informationen aus Low-Fidelity-Modellen reduziert. Diese werden mit einigen wenigen, intelligent gewählten Auswertungen des Referenzmodells kombiniert, um genaue Schätzungen zu einem Bruchteil der Kosten im Vergleich zu aktuellen UQ-Methoden zu erhalten, vgl. Abbildung 1. Darüber hinaus können durch einen Bayes'schen Ansatz Intervalle berechnet werden, die das Vertrauen in die Schätzungen quantifizieren und adaptive Verfeinerungen ermöglichen. Weiterhin soll der vorgeschlagene UQ-Ansatz als Grundlage für die Entwicklung eines neuartigen stochastischen Optimierungsframeworks für das Design komplexer Strukturen und Systeme unter Unsicherheiten dienen. Das geplante Framework und die vorgeschlagenen Methoden sind sehr allgemein und werden auf ein breites Spektrum von Problemen anwendbar sein. Wir werden einige reale Multiphysics-Systeme betrachten, beispielsweise stark gekoppelte Fluid-Struktur-Wechselwirkungs-Probleme und Multiphysics-Anwendungen, die im Zusammenhang mit dem selektiven Laserschmelzen auftreten.

© Figure 1

Abbildung 1: Schematische Darstellung der Korrelation zwischen Low-Fidelity-Modell und High-Fidelity-Modell

Leitung

© Prof. Wolfgang Wall

Prof. Wolfgang Wall
Leiter des Lehrstuhls für Numerische Mechanik
Technische Universität München

© Prof. Pheadon Koutsourelakis

Prof. Phaedon-Stelios Koutsourelakis
Inhaber der Professur für Kontinuumsmechanik
Technische Universität München

Bearbeiter

© JonasNitzler.jpg

M.Sc. Jonas Nitzler
Prof. für Kontinuumsmechanik
Lehrstuhl für Numerische Mechanik
Technische Universität München

Veröffentlichungen

• Nitzler, J.; Biehler, J.; Fehn, N.; Koutsourelakis, P.-S.; Wall, W. A.:
   Generalized Probabilistic Learning Approach for Multi-Fidelity Uncertainty Propagation in Complex Physical Simulations, 2020 Link
• Biehler, J.; Mäck, M.; Hanss, M.; Koutsourelakis, P.-S.; Wall, W. A.:
  Multifidelity approaches for uncertainty quantification, 2019
  GAMM - Mitteilungen 42 (2) Link