Eine hybride Sampling-Stochastische-Finite-Element-Methode für polymorphe, mikrostrukturelle Unsicherheiten in heterogenen Materialien
Eine Weiterführung des Themas findet aktuell in der zweiten Bearbeitungsphase statt.
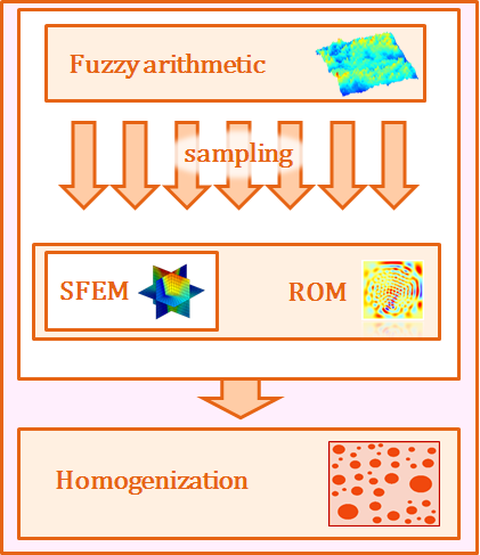
Project Flow: Establishing a combination of SFEM, ROM and Fuzzy Arithmetic and its application to Computational Homogenization problems.
Das übergeordnete Ziel dieses Vorhabens auf der Methodenseite ist es, eine vom Rechenaufwand handhabbare numerische Methode zu etablieren, die es erlaubt, polymorphe Unsicherheiten in großdimensionierten Problemen (die z.B. im Rahmen der numerischen Analyse der Mikrostruktur heterogener Materialien entstehen) zu erfassen. Dazu wird die Methode auf der einen Seite unscharfe Wahrscheinlichkeitsverteilungen der Zufallsparameter (die die Geometrie der Mikrostruktur beschreiben) berücksichtigen und auf der anderen Seite wird die Methode nur auf wenigen reduzierten Basismoden beruhen. Diese Bausteine werden es ermöglichen, zusätzlich zu epistemischen auch aleatorische Unsicherheiten in einer numerisch zugänglichen Art und Weise zu behandeln. Das übergeordnete Ziel dieses Vorhabens auf der Anwendungsseite ist es, ein nicht-deterministisches, makroskopisches Materialmodel zu etablieren. Das Model wird einerseits der Heterogenität der dem Material zugrundeliegenden Mikrostruktur durch numerische Homogenisierung Rechnung tragen und andererseits polymorphe Unsicherheiten in der Geometriebeschreibung der Mikrostruktur erfassen. Das so formulierte nicht-deterministische, makroskopische Materialmodel stellt somit den notwendigen Startpunkt für den Entwurf makroskopischer Ingenieurstrukturen unter Berücksichtigung polymorpher Unsicherheiten in der Beschreibung der, heterogenen Materialien zugrundeliegenden, Mikrostruktur dar.
Zusammenfassung der Projektergebnisse
Die effektiven makroskopischen Eigenschaften heterogener Materialien ergeben sich aus der Antwort der zugrunde liegenden Mikrostruktur und können entweder durch analytische oder numerische Homogenisierung geschätzt werden. Analytische Homogenisierungsverfahren zur Bestimmung des makroskopischen Verhaltens heterogener Materialien sind oft auf lineare Probleme beschränkt. Im Gegensatz dazu kann die numerische Homogenisierung auf anspruchsvolle, beliebige lineare und nichtlineare Probleme angewendet werden.
Die numerische Homogenisierung erfordert zwei getrennte Finite-Elemente-Modelle: ein makroskopisches Modell der Makrostruktur (das Baukonstruktionsproblem) und ein mikroskopisches Modell der den Werkstoffen zugrunde liegenden Mikrostruktur. Dabei beinhaltet die numerische Homogenisierung zwei Hauptbestandteile: die Übertragung der makroskopischen Belastung auf die Mikroebene und die Mittelwertbildung der entsprechenden Antwort der Mikrostruktur, um die effektiven makroskopischen Eigenschaften zu erhalten. Die Übertragung der makroskopischen Belastung auf die Mikroskala kann z.B. durch Anwendung von Neumann-, periodischen oder Dirichlet-Randbedingungen (die die Hill-Mandel-Bedingung erfüllen) auf die Mikrostruktur erfolgen.
Ein technisch anspruchsvoller Aspekt für die numerische Homogenisierung ist die korrekte Modellierung der Materialmikrostruktur. Bei Werkstoffen mit Unschärfen in der Mikrostruktur, die in diesem Projekt berücksichtig werden, ist dieses Problem noch schwieriger.
Das Ziel von Phase I ist die Entwicklung eines Fuzzy-stochastischen FEM-basierten Frameworks zur numerischen Homogenisierung heterogener Materialien mit polymorphen Unschärfen in der Mikrostruktur. Insbesondere liegt der Schwerpunkt auf der effizienten und genauen Simulation der Mikrostuktur mit polymorphen Unschärfen.
In Phase I des Projekts entwarfen wir zunächst ein fuzzy-stochastisches Benchmark-Beispiel für eine Mikrostruktur heterogener Materialien mit unscharf verteilten Einschlüssen. Darauf aufbauend etablierten wir die folgenden neuartigen Techniken für stochastische und fuzzy-stochastische Probleme:
- Isoparametrische stochastische lokale FEM
- Isoparametrische fuzzy lokale FEM
- fuzzy eXtended FEM
- Isoparametrische fuzzy-stochastische lokale FEM
- Fuzzy-stochastische eXtended FEM
Wir führten Simulationen mit hybrider sampling-spektraler fuzzy-stochastischer FEM und vollspektraler fuzzy-stochastischer FEM durch. Für die Ordnungsreduktion im stochastischen Bereich führten wir
- die globale Galerkin-Methode mit eXtended Fourier-Basis,
- das reduzierte Modell basiert auf Eigenvektoren eines deterministischen Hilfsproblems,
- die Benutzung der POD und der stochastischen lokalen FEM sowie
- elementbasierte diskrete empirische Approximation
ein.
Um die Lösung zu beschleunigen und teures fuzzy Sampling zu vermeiden, haben wir darüber hinaus eine Methode entwickelt, die auf einem äquivalenten Modell mit reduzierten Dimensionen basiert.
Wesentliche Projektresultate
- Entwicklung eines korrekten stochastischen FEM-Frameworks für aleatorische Unschärfe
- Entwicklung eines hybriden fuzzy-stochastischen FEM-Frameworks für polymorphe Unschärfe
- Integration der ROM in die stochastische FEM
- Integration der ROM in die hybride fuzzy-stochastische FEM
- Anwendung auf ein Benchmark-Beispiel für Materialien mit unscharfen Mikrostruktureigenschaften

Hr. Pivovarov
Dmytro Pivovarov, M. Sc.
Friedrich-Alexander-Universität
Erlangen-Nürnberg
Lehrstuhl für Technische Mechanik (LTM)
-
Pivovarov, D., Zabihyan, R., Mergheim, J., Willner, K., Steinmann, P.:
On periodic boundary conditions and ergodicity in computational homogenization of heterogeneous materials with random microstructure, Computer Methods in Applied Mechanics and Engineering 357, 112,563 (2019) -
Pivovarov, D., Steinmann, P., Willner, K.:
Acceleration of the spectral stochastic fem using pod and element based discrete empirical approximation for computational homogenization of heterogeneous materials with random geometry, Computer Methods in Applied Mechanics and Engineering pp 112-689 (2019) -
Pivovarov, D., Hahn, V., Steinmann, P., Willner, K., Leyendecker, S.:
Fuzzy dynamics of multibody systems with polymorphic uncertainty in the material microstructure, Computational Mechanics 64 (6), pp 1601–1619 (2019) -
Pivovarov, D., Oberleiter, T., Willner, K., Steinmann, P.:
Fuzzy-stochastic fem-based homogenization framework for materials with polymorphic uncertainties in the microstructure, International Journal for Numerical Methods in Engineering 116 (9), pp 633–660 (2018) -
Pivovarov, D., Steinmann, P., Willner, K.:
Two reduction methods for stochastic fem based homogenization using global basis functions, Computer Methods in Applied Mechanics and Engineering 332, pp 488 – 519 (2018) - Pivovarov, D., Willner, K., Steinmann, P.:
On spectral fuzzy-stochastic fem for problems involving polymorphic geometrical uncertainties, Computer Methods in Applied Mechanics and Engineering 350,
pp 432–461 (2018)


