Polymorphe Unschärfemodellierung zur Stabilitätsuntersuchung flüssigkeitsgesättigter Böden und Erdbauwerke
Eine Weiterführung des Themas findet aktuell in der zweiten Bearbeitungsphase statt.
Der Kernbereich des Projektes ist die Erfassung und Bewertung polymorpher Unschärfen in numerischen Berechnungssimulationen für grundbauspezifische Fragestellungen, speziell flüssigkeitsgefüllter poröser Böden. Zur Beschreibung des stark gekoppelten Antwortverhaltens wird die Theorie poröser Medien (TPM) eingesetzt und zur numerischen Lösung allgemeiner Rand- und Anfangswertprobleme im Rahmen der der Finiten Element Methode (FEM) aufbereitet. Ziel des Forschungsprojektes ist die Erweiterung der deterministischen Strukturanalyse um zwei vielversprechende Ansätze der Sensitivitätsanalyse zur Erfassung der Einflüsse der unterschiedlichen Unschärfen auf das Berechnungsergebnis. Zusätzlich sollen die Sensitivitäten der Unschärfen verglichen und bewertet werden um Anwendern langfristig effizientere Methoden zur Bemessung von Erdbauwerken zur Verfügung stellen zu können.
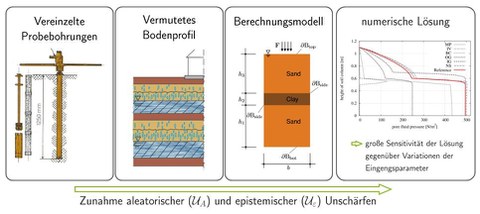
Unschärfe-Quellen im Modellierungsprozess (beispielhaft für ein Konsolidierungsproblem)
Am Beispiel eines einfachen Konsolidierungsproblems ist bereits eine große Sensitivität der numerischen Lösung gegenüber Variationen der Material- und Anfangswerte erkennbar, siehe Abb.1. Diese und weitere Sensitivitäten sollen langfristig anhand der variationellen sowie der probabilistischen Sensitivitätsanalyse quantifiziert werden können. Die variationelle oder auch „direkte“ Sensitivitätsanalyse ist ein aus der Optimierung stammender Ansatz und berechnet analytisch/numerisch den Einfluss der einzelnen Parameter als stetige Funktionen. Der Vorteil liegt in der akkuraten Darstellung des Lösungsraums und der effizienten Berechnung, der Nachteil in der aufwändigen Erstellung und algorithmischen Umsetzung. Eine Alternative bietet die probabilistische Sensitivitätsanalyse aus dem Bereich der Statistik. Der Aufwand wächst hierbei lediglich proportional zur Dimension des Problems. Den Modellparametern wird anstelle eines festen Wertes eine Wahrscheinlichkeitsverteilung zugeordnet, aus der zufällig Werte gezogen werden. Dadurch entsteht in mehreren Simulationsdurchläufen ein Datensatz, anhand dessen eine Sensitivitätsanalyse durchführbar ist. Hierbei werden verschiedene Ansätze der Bayes-Statistik verwendet, die es erlauben anhand einer relativ geringer Anzahl an Simulationen eine Vielzahl an Sensitivitätsmessungen durchzuführen. Genauer soll mit Hilfe einer Gauß-Prozess Regression ein Metamodell erstellt werden und anhand der resultierenden Posteriori-Verteilung eine Sensitivitätsanalyse, abhängig von der Wahl der A-priori-Verteilungen, durchgeführt werden. Beide Ansätze werden verfolgt und hinsichtlich ihrer Vor- und Nachteile untersucht, verglichen und bewertet. Langfristig sollen komplexere Fragestellungen durch Weiterentwicklung der Modelle bearbeitet werden können. Abbildung 2 zeigt chronologisch die Ziele des Teilprojektes für die erste Projektphase.
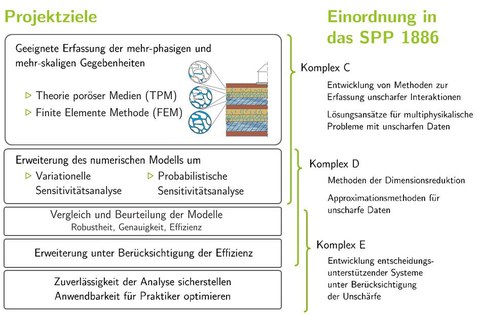
Zielsetzung des Teilprojekts für die erste Projektphase
Zusammenfassung der Projektergebnisse
Das grundlegende Ziel war und ist die Charakterisierung und Analyse des Einflusses polymorph
unscharfer Daten auf die deterministische Modellierung des multi-physikalischen Verhaltens gesättigten Bodens. Hierfür haben wir als Benchmark ein Konsolidierungs-Anfangswertproblem gewählt, um sowohl bestehende als auch selbst entwickelte Methoden daran zu testen und vergleichen zu können.
Ein Zwei-Phasen-Modell (Festkörper und Fluid, beides materiell inkompressibel und linear elastisch) wurde im Rahmen der Theorie poröser Medien aufbereitet, sodass die sonst klassisch deterministischen FEM-Berechnungen automatisiert mit probabilistischen und stochastischen Ansätzen berechnet werden können (in FEAP). Darüber hinaus haben wir ein benutzerfreundliches Werkzeug (in R) für die Erzeugung von Zufallsfeldern mit unterschiedlichen Eigenschaften entwickelt. Das Werkzeug ermöglicht die Modellierung aleatorischer Unschärfen wie Bodeneigenschaften für mehrere Bodenschichten sowie epistemische Unschärfen wie die Anzahl der Schichten, ihre Positionen und Geometrien. Für die praktische Umsetzung zwischen R und FEAP wurde ein Shell-Skript erstellt, das die automatisierte Organisation und Verarbeitung der einzelnen Serien von Zufallsfeldern steuert und die Ausgaben des TPM-Modells in einem geeigneten und sortierten Format für die folgenden Analysen zur Verfügung stellt. Mithilfe des Monte-Carlo-Ansatzes haben wir die Entwicklung des Fluidporendrucks über die Zeit sowie die Setzungen aufgrund variierender Oberflächenbelastungen und Eigengewicht analysiert. Darüber hinaus wurde die kombinierte Auswirkung einer Variation der Korrelationslängen und der natürlichen Variabilität der Eigenschaften durch einen fuzzy-probabilistischen Ansatz untersucht.
Neben diesen globalen Unschärfequantifizierungsansätzen lag ein weiterer Schwerpunkt auf der Entwicklung der variationellen Sensitivitätsanalyse für das zugrunde liegende physikalische Modell (TPM), die den lokalen Unschärfequantifizierungsmethoden zugeordnet werden kann. Die theoretische Herleitung der Modellgleichungen sowie die Implementierung in FEAP führten zu einem effizienten Algorithmus, der mit nur einer deterministischen Berechnung weitreichende Informationen über die Sensitivität des betrachteten Problems liefert. Für die geeignete Auswertung und Beurteilung wurden unterschiedliche Sensitivitätsmaße entwickelt, die Aufschluss über den Einfluss einzelner Parameter (globale Einflussanalyse) aber auch die räumliche Verteilung eines Parameters geben (lokale Einflussanalyse). Die Vor- und Nachteile der unterschiedlichen Methoden wurden anhand umfassender Berechnungen und Auswertungen ausgearbeitet.
Parallel wurde die DEIM-Methode für die TPM aufbereitet, um den Rechenaufwand für Analysen zu reduzieren, die eine hohe Anzahl an Modelldurchläufen erfordern.
Wesentliche Projektresultate
-
Variationelle Sensitivitätsanalyse der Theorie poröser Medien für ein Zwei-Phasen-Modell (Festkörper/Fluid)
-
Monte-Carlo-Methode mit Random Fields
-
Fuzzy-probabilistische Untersuchungen polymorpher Unschärfen
-
Analyse der Vor- und Nachteile der unterschiedlichen Herangehensweisen
-
Entwicklung benutzerfreundlicher Tools zur Anwendung von Unschärfequantifizierungsmethoden
-
Lösung von Schnittstellenproblematiken zwischen FEAP und R
-
Umsetzung von Reduktionsmethoden (insbesondere DEIM) für die Theorie poröser Medien zur Beschleunigung der Modelldurchläufe

Prof. Ricken
Prof. Dr.-Ing. Tim Ricken
Universität Stuttgart
Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen
Fakultät für Luft- und Raumfahrttechnik und Geodäsie

Prof. Ickstadt
Professor Dr. Katja Ickstadt
Technische Universität Dortmund
Fakultät Statistik
Lehrstuhl für mathematische Statistik und biometrische Anwendungen

Fr. Henning
Carla Henning, M.Sc.
Universität Stuttgart
Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen
Fakultät für Luft- und Raumfahrttechnik und Geodäsie

Fr. Herbrandt
Swetlana Herbrandt
Technische Universität Dortmund
Fakultät Statistik
Lehrstuhl für mathematische Statistik und biometrische Anwendungen
- Henning, C., Ricken, T.:
Polymorphic Uncertainty Quantification of Computational Soil and Earth Structure Simulations via the Variational Sensitivity Analysis,
(PAMM) 2019, Link - Pivovarov, D., Willner, K., Steinmann, P., Brumme, S., Müller, M., Srisupattarawanit, T., Reese, S.:
Challenges of order reduction techniques for problems involving polymorphic uncertainty, (GAMM -Mitteilungen) 42 (2) 2019, Link - Drieschner, M., Matthies, H. G., Hoang, T. V., Rosić, B. V., Ricken, T., Henning, C., Weinberg, K.:
Analysis of polymorphic data uncertainties in engineering applications,
(GAMM-Mitteilungen) 2019, Link - Schmidt, A., Henning, C., Herbrandt, S., Könke, C., Ickstadt, K., Ricken, T., Lahmer, T.: Numerical studies of earth structure assessment via the theory of porous media using fuzzy probability based random field material descriptions,
(GAMM-Mitteilungen) 42 (1) 2019, Link - Henning, C., Herbrandt, S., Ickstadt, K., Ricken, T.:
Combining Finite Elements and Random Fields to Quantify Uncertainty in a Multi‐phase Structural Analysis (PAMM) 18 (1) 2018, Link - Henning, C., Ricken, T.:
Polymorphic uncertainty quantification for stability analysis of fluid saturated soil and earth structures, (PAMM) 17 (1) 2017, pp 59-62 Link
