Polymorphic uncertainty of friction
In the fields of mechanical engineering, friction is ubiquitous. It is a fundamental cause of energy loss and wear. Another concern is the occurrence of comfort-relevant friction induced vibrations. Prominent examples of this are NVH phenomena such as brake squeal, which is being investigated at great expense by the German automotive industry and academia, to determine its causes and potential influencing factors.
For this purpose, numerous specialized measurements are performed, and models of varying complexity are used. All of these measurements and models have the common trait that the coefficient of friction, defined as the ratio of the tangential force and normal force, has a decisive influence on the systems stability.
To parameterize the friction coefficient in macroscopic models, measurements must be performed. In this case, often an average over time and over various loading procedures is used. As the measurements reveal, the coefficient of friction is in reality not constant, but is subject to a high degree of dynamics on various time scales, caused by complex processes in the boundary layer. A treatment of the coefficient of friction as a steady-state parameter, or even as a constant, is thus a major reduction.
The large variability of the coefficient of friction causes a corresponding variance in the stability limits of the models considered. This phenomenon is observed in the real world, where squealing seems to have a non-deterministic behavior. This suggests uncertainties in the modeling of the friction coefficient. Due to the various types of uncertainty (variability, incompleteness and inaccuracy), the entire problem is a matter of polymorphic uncertainty.
The proposed project focuses on the modeling of the friction coefficient, taking into account the various causes of uncertainty. Selections of raw data obtained at the applicants institute throughout many years of research on friction phenomena in brake systems will be evaluated and classified with respect to its uncertainty properties.
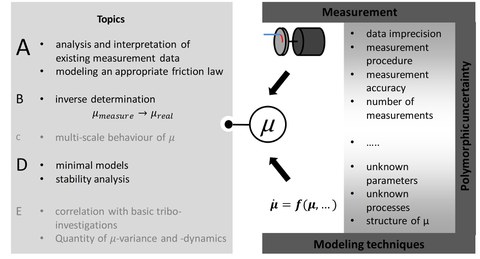
Uncertainties in friction and main topics of the project
With the aid of these findings, appropriate descriptions of the coefficient of friction will be developed by means of polymorphic uncertainty models. In particular, this refers to the structure of the equations (for example, order of the system of differential equations), and the dependencies on external parameters (for example, normal force, relative speed).
The uncertainty model of the friction coefficient will be tested based on minimal models of brake squeal in both the frequency and time domains. The impact of relevant dependencies on stability will be emphasized. This technique should be a basis for future work, as it will facilitate the attainment of statistically reliable statements regarding the relevance and frequency of occurrence of friction induced instabilities, based on relatively few measurement applications.

Prof. Ostermeyer
Prof. Dr.-Ing. habil. Georg Peter Ostermeyer
Technische Universität Braunschweig
Institut für Dynamik und Schwingungen


