Efficient Bayesian Multi-fidelity Schemes for Analysis and Design of Complex Multiphysics Systems
The goal within this project is the development of a general-purpose uncertainty quantification framework for complex, real-world multi-physics problems with high stochastic dimension, based on novel Bayesian multi-fidelity approaches to achieve unprecedented overall efficiency and accuracy. Moreover, it is planned to extend the developed framework towards a stochastic optimization tool which can be used to perform robust design of structures and systems under uncertainty.
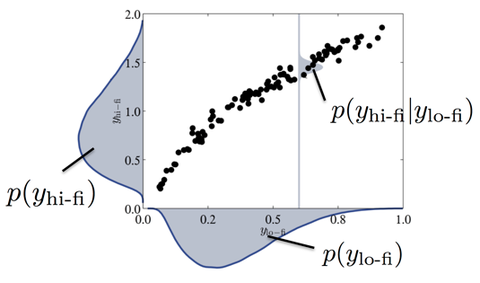
The developed set of UQ methods will be able to handle complex, real-world structures and systems, characterized by high-dimensional parametric uncertainties arising from the discretization of multi-dimensional, non-Gaussian random fields. The methods will provide certifiable estimates for the statistics of the output Quantities of Interest (QoI), as well as sensitivity measures for the different uncertain model input parameters. The hitherto prohibitive computational costs associated with UQ in such complex and challenging settings will be mitigated by rigorously incorporating information from inexpensive, lower-fidelity models. These are combined with a few, intelligently selected evaluations of the reference, expensive, high-fidelity model, in order to obtain accurate estimates at a fraction of the cost compared to current UQ methods, cf. Figure 1. Moreover, by adopting a Bayesian approach, credible intervals can be computed which quantify the confidence in the estimates as well as guide adaptive refinements. In addition, the UQ approach advocated will serve as the basis for the development of a novel stochastic optimization framework for the design of complex structures and systems in the presence of uncertainties. The proposed framework and methods are very general and will be applicable to a wide range of problems. We will consider several of real-world multi-physics systems, e.g., examples involving strongly coupled fluid-structure-interaction and multi-physics applications arising in the context of selective laser melting.
Figure 1. Schematic representation of correlation between low-fidelity and high-fidelity model output

Prof. Wolfgang Wall
Prof. Wolfgang Wall
Leiter des Lehrstuhls für Numerische Mechanik
Technische Universität München

Phaedon-Stelios Koutsourelakis
Prof. Phaedon-Stelios Koutsourelakis
Inhaber der Professur für Kontinuumsmechanik
Technische Universität München

Jonas Nitzler
M.Sc. Jonas Nitzler
Prof. für Kontinuumsmechanik
Lehrstuhl für Numerische Mechanik
Technische Universität München
- Publication 1