Mehrskalige Versagensanalyse unter polymorphen Unsicherheiten für das optimale Design von Rotorblättern
Eine Weiterführung des Themas findet aktuell in der zweiten Bearbeitungsphase statt.
Hauptziele sind die Identifikation von polymorphen Unsicherheiten beim Strukturdesign von Rotorblättern und die Entwicklung von nichtdeterministischen Mehrskalenmodellen (in Raum und Zeit) mit entsprechenden effizienten numerischen Verfahren, die diese Unsicherheiten in die typische Kette „Design – Test – Implementation – Wartung“ integrieren.
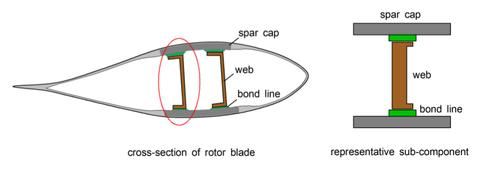
Querschnitte eines Rotorblattes und eines repräsentatives Bauteils für die Untersuchungen an Verklebungen
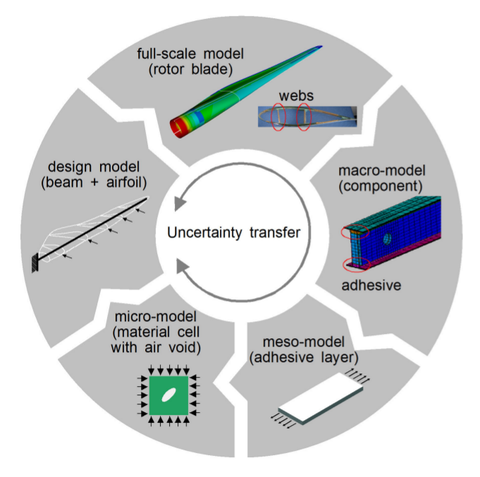
Mehrskalenanalyse bei der Untersuchung von Rotorblättern
- Identifikation und Beschreibung polymorpher Unsicherheiten beim Design von Rotorblättern. (Fuzzy and probabilistic methods)
- Beschreibung des Gesamtmodells und Aufteilung in strukturelle Teilkomponenten mit polymorphen Unsicherheiten und Entwicklung von FE Simulationen. (FE, Monte Carlo, stochastic FE)
- Modellierung von Unsicherheiten im makroskopischen Komponentenmodell. Dies betrifft insbesondere die Klebeschicht mit homogenisiertem Material unter unscharfen Materialparametern. (multiscale FE, numerical upscaling, model reduction, tensor methods)
- Modellierung von mehrskaligen Ermüdungsprozessen.
- Mesoskopische Modellierung und Simulation der nicht-deterministischen Verleimungsschicht mit Klebekontakt.
- Entwicklung und Validierung eines Komponentensimulators.
- Validierung und Integration von Komponenten zum Gesamtmodel.
Zusammenfassung der Projektergebnisse
Die Qualität von Klebverbindungen in Rotorblättern von Windenergieanlagen hat einen maßgeblichen Einfluss auf die ganzheitliche Strukturintegrität und -zuverlässigkeit. Herstellungsbedingte Ungenauigkeiten und Imperfektionen können zu schlechter Haftung der Systemkomponenten und kritischen Luftporen in den Klebeschichten führen, für welche im Rahmen der ersten Förderphase experimentelle und numerische Untersuchungen durchgeführt wurden.
Dafür wurde ein Mehrskalenproblem bestehend aus Makro-, Meso- und Mikroskala definiert. Als Makromodell dient der Henkelbalken, eine vom Fraunhofer IWES entwickelte repräsentative Subkomponente zur Analyse von Klebverbindungen in Rotorblättern. Auf der Mesoskala wurden gelochte zwei- bzw. dreidimensionale Gebiete als Ersatzmodelle für Klebeschichten verwendet und einzelne Zellen mit Luftpore innerhalb der Klebeschicht definieren die Mikroskala.
Mittels zur Verfügung stehender Bilddateien aus computertomographischen Untersuchungen vom Henkelbalken konnten Lufteinschlüsse identifiziert werden. Durch verschiedene Bildverarbeitungstechniken wurden die ZfP-Daten analysiert, aufbereitet und zur Modellierung unscharfer Parameter wie Anzahl, Lage, Form und Größe verwendet. Dafür wurde ein allgemeingültiges Konzept hinsichtlich Datenakquisition, -modellierung, -verarbeitung und -assimilation im Rahmen des Komplexes A entwickelt und in Kooperation mit anderen Forschungsgruppen des SPP 1886 zusätzlich auf unterschiedliche Ingenieurprobleme angewendet.
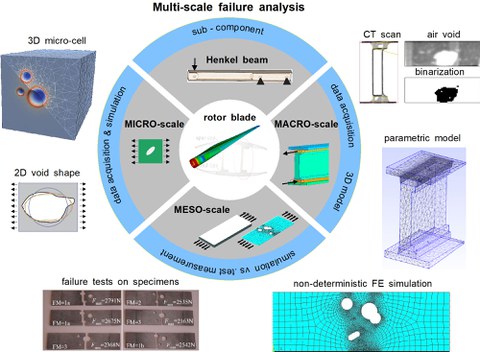
Konzept der Versagensanalyse auf mehreren Skalen unter polymorphen Unsicherheiten
Die Integration der akquirierten Daten in das parametrisierte 3D-Modell des Henkelbalkens führte zu FE-Simulationen unter polymorpher Unschärfe. Für die Quantifizierung wurden probabilistische sowie nicht-probabilistische Methoden verwendet. Die gleichzeitige Berücksichtigung von stochastischen, Intervall- und Fuzzy-Variablen machten folglich die Entwicklung und Anwendung effizienter numerischer Verfahren unabdingbar. Die Klebeschichten mit Luftporen als Mesomodell wurden mittels Guyan-Reduktion aus dem Gesamtmodell extrahiert. Für die Berücksichtigung der Luftporen konnten parametrische Gebietszerlegungsverfahren basierend auf der Schwarz-Methode, der Schurkomplement-Methode oder der FETI-DP-Methode erfolgreich implementiert werden. Damit wurden die Luftporen mit polymorph unscharfen Parametern auf Mikroskala nahezu entkoppelt, was zu einem effizienten mehrskaligen Modell des Henkelbalkens führt. Dennoch war es zweckmäßig, Approximationsmethoden zur Berücksichtigung der polymorphen Unschärfe zu untersuchen. Für die beschriebene Anwendung konnten künstliche neuronale Netze (ANNs) mit guter Übereinstimmung zur aufwendigen Referenzlösung definiert werden.
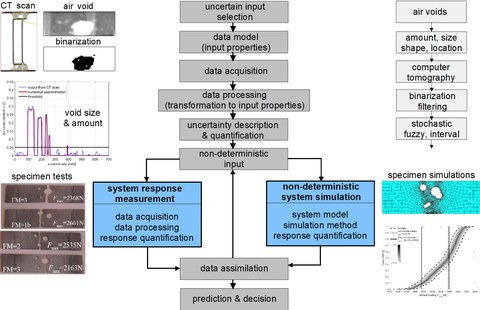
Allgemeiner Ansatz zur Datenerfassung, Modellierung und Assimilation bei technischen Problemen
Zur Validierung der beschriebenen numerischen Verfahren und Modelle wurden experimentelle Untersuchungen an einem repräsentativen Mesoskalenproblem durchgeführt. Eine Reihe von Plexiglas-Scheiben mit nahezu ähnlichen Eigenschaften wurde hergestellt und uniaxial auf Zug belastet. Unterschiedliche Versagensmodi bei unterschiedlichen Versagenslasten konnten identifiziert werden und begründeten die Verwendung unscharfer Daten in numerischen Simulationen. Die experimentellen Ergebnisse wurden durch die Numerik qualitativ sowie quantitativ erfasst. Aufwendige FE-Simulationen konnten mittels ANNs unter Vernachlässigung geringfügiger Abweichungen effizient ersetzt werden. Die unscharfen Parameter wurden als stochastische und/oder Fuzzy-Variablen definiert. Es zeigte sich, dass die gleichen ANNs unabhängig von der Art der unscharfen Daten zufriedenstellend angewendet werden können.
Zusätzlich wurden mit anderen Forschungsgruppen innerhalb des SPP 1886 repräsentative Untersuchungen zur Bewertung, Entscheidungsfindung und Entscheidungsverbesserung unter polymorpher Unschärfe durchgeführt. Diese werden in der zweiten Förderphase in Hinblick auf reale Ingenieurprobleme angewendet und weiter intensiviert.
Wesentliche Projektresultate
-
Identifikation von Luftporen in Klebverbindungen mittels zerstörungsfreier Prüfverfahren (ZfP)
-
Entwicklung eines allgemeingültigen Konzeptes hinsichtlich Datenakquisition, -modellierung, -verarbeitung und -assimilation für Ingenieurprobleme
-
Definition eines Mehrskalenproblems bestehend aus Makro-, Meso- und Mikroskala
-
Aufbau eines parametrisierten 3D-Modells des Henkelbalkens und FE-Simulationen unter polymorpher Unschärfe
-
Entwicklung effizienter numerischer Verfahren zur Behandlung hochdimensionaler Probleme, z.B. adaptive parametrische Gebietszerlegungsverfahren oder hierarchische Niedrigrang-Tensorformate
-
Aufbau von künstlichen neuronalen Netzwerken (ANNs) und Verwendung für Probleme mit unscharfen Daten, insbesondere der Ermittlung und Lokalisierung von Spannungskonzentrationen in Gebieten mit Löchern
-
Vergleich von numerischen und experimentellen Untersuchungen an einem repräsentativen Ersatzproblem auf Mesoskala
-
Durchführung von Untersuchungen zur Bewertung, Entscheidungsfindung und Entscheidungsverbesserung unter polymorpher Unschärfe

Robert Gruhlke
Robert Gruhlke
Weierstraß-Institut

M. Sc. Martin Drieschner
M.Sc. Martin Drieschner
Technische Universität Berlin
Fachgebiet Statik und Dynamik
- Drieschner, M.; Petryna, Y.; Gruhlke, R.; Eigel, M.; Hömberg, D.:
Fachzeitschrift: Comparison of various monomorphic and polymorphic approaches for uncertainty quantification with experimental investigations. Reliability Engineering and System Safety, 2020 (accepted) - Drieschner, M.; Petryna, Y.; Freitag, S., Edler, P.; Schmidt, A.; Lahmer, T.:
Fachzeitschrift: Decision making and design in structural engineering problems under polymorphic uncertainty, 2020 (in review) - Drieschner, M.; Petryna, Y.; Kähler, P.:
Fachzeitschrift: Decision making in structural engineering problems under polymorphic uncertainty - A benchmark proposal (version 3), Preprint-Reihe des Fachgebiets Statik und Dynamik, Technische Universität Berlin, Preprint No. 2019-03 2020 Link - Drieschner, M.; Gruhlke, R.; Petryna, Y.; Eigel, M.; Hömberg, D.:
Analysis of model and data uncertainties for the failure of adhesive bonds in composite materials. Proc. Appl. Math. Mech. (in review) - Eigel, M.; Grasedyck; L.; Gruhlke, R.; Moser, D.:
Fachzeitschrift: Low rank surrogates for polymorphic fields with application to fuzzy-stochastic partial differential equations, 2019 (in review) - Eigel, M.; Gruhkle, R.:
A hybrid FETI-DP method for non-smooth random partial differential equations, 2019 (in review) - Drieschner, M.; Matthies, H.G.; Hoang, T.-V.; Roisc, B.; Ricken, T.; Ostermeyer, G.-P.; Müller, M.; Brumme, S.; Srisupattarawanit, T.; Weinberg, K.; Korzeniowski, T.F.:
Analysis of polymorphic data uncertainties in engineering applications, GAMM - Mitteilungen 2019 Link - Papaioannou, I.; Daub, M.; Drieschner, M.; Duddeck, F.; Ehre, M.; Eichner, L.; Eigel, M.; Götz, M.; Graf, W.; Grasedyck, L.; Gruhlke, R.; Hömberg, D.; Kaliske; M.; Moser, D.; Petryna, Y.; Straub, D.:
Assessment and design of an engineering structure with polymorphic uncertainty quantification, GAMM - Mitteilungen 2019 Link - Gruhlke, R.; Drieschner, M.; Eigel, M.; Hömberg, D.; Petryna, Y.:
Artificial Neural Network forecasting for monomorphic and polymorphic uncertainty models and comparison with experimental investigations, In Proc. Appl. Math. Mech. 2019 Link - Drieschner, M.; Petryna, Y.; Gruhlke, R.; Eigel, M.; Hömberg, D.;
Failure analysis of adhesive bonds with polymorphic uncertainties: Experiment and simulation, ECCM-ECFD 2018, Glasgow (accepted) - Gruhlke, R.; Eigel, M.; Hömberg, D.; Drieschner, M.; Petryna, Y.:
A hybrid stochastic domain decomposition method for partial differential equations with localised possibly rough random data, In Proc. Appl. Math. Mech. 2018 Link - Petryna, Y.; Drieschner, M.:
Data for: Decision making in structural engineering problems under polymorphic uncertainty - a benchmark proposal, 2019 Mendeley Data, v4 Link - Drieschner, M.; Eigel, M.; Gruhlke, R.; Hömberg, D.; Petryna, Y.:
Comparison of monomorphic and polymorphic approaches for uncertainty quantification with experimental investigations, 2019 WIAS-Preprint No.2579 Link - Eigel, M.; Gruhlke, R.; Marschall, M.:
Low-rank tensor reconstruction of concentrated densities with application to Bayesian inversion, 2019 WIAS-Preprint No. 2672 Link - Petryna, Y.; Drieschner, M..:
Decision making in structural engineering problems under polymorphic uncertainty - A benchmark proposal, Preprint-Reihe des Fachgebiets Statik und Dynamik, Technische Universität Berlin, Preprint No. 2019-03 Link - Drieschner, M.; Petryna, Y.; Eichner, L.:
Parameterization of arbitrary hole shapes using non-destructive testing and resulting stress concentration in a 2D plate with finite dimensions, Preprint-Reihe des Fachgebiets Statik und Dynamik, Technische Universität Berlin, Preprint No. 2019-02 Link - Drieschner, M.; Petryna, Y.:
Acquisition of polymorphic uncertain data based on computer tomographic scans and integration in numerical models of adhesive bonds, Preprint-Reihe des Fachgebiets Statik und Dynamik, Technische Universität Berlin, Preprint No. 2019-01 Link - Eigel, M.; Gruhlke, R.:
A hybrid FETI-DP method for non-smooth random partial differential equations, 2018 WIAS-Preprint No. 2565 Link



