Polymorphic uncertainty modeling for stability quantification of fluid saturated soil and earth structures
A continuation of the topic is currently taking place in the second project phase.
The focus of the project is on quantification and assessment of polymorphic uncertainties in computational simulations for earth structures, especially for fluid-saturated soils. To describe the strongly coupled response behavior, the theory of porous media (tpm) will be used and prepared within the framework of the finite element method (fem) for the numerical solution of initial and boundary value problems. The main objective of the research project is the enhancement of the deterministic structural analysis through two promising approaches of the sensitivity analysis to capture impacts of the different uncertainties on computational results. Additionally the sensitivities of uncertainties will be compared and rated to develop more efficient methods and tools for the sizing of earth structures in the long-run.
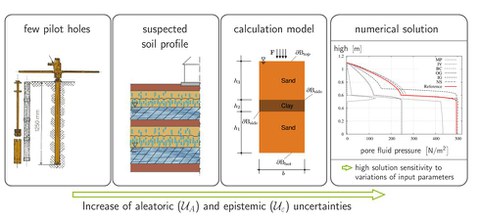
Sources of Uncertainties during the modeling process (exemplary for a consolidation problem)
A simple consolidation problem already provided a high sensitivity in the computational results towards variation of material parameters and initial values, see fig.1. The variational and probabilistic sensitivity analyses enable to quantify these sensitivities. The variational sensitivity analysis is a tool for optimization procedures, which captures the impact of different parameters as continuous functions. One advantage is the accurate approximation of the solution space and the efficient computation time, a disadvantage lies in the analytical derivation and algorithmic implementation. Another approach is given by the probabilistic sensitivity analysis from the field of statistics. The expense only increases proportionally to the problems dimension. Instead of a constant value, the model parameters are defined as probability distribution, which provides random values. Thus a set of solution data is built up by several cycles of the simulation. By means of this data base, the probabilistic sensitivity analysis can be applied. Different approaches of the Bayes statistics will enable to receive accurate information with just a few simulations. In detail, the gaussian process regression will be used to create a meta model. By means of the resulting posteriori-distribution the sensitivity analysis will be performed, depending on the choice of the a-priori-distribution. Both approaches will be pursued and advantages and disadvantages will be captured and compared, so that more complex problems can be handled in the long run through further development of the models. Figure 2 shows the objectives of this project chronologically for the first period.
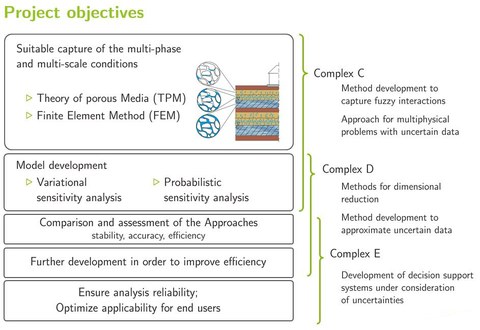
Objectives of the first period
Summary of the first funding phase
The fundamental objective was and is to characterize and analyze the influence of polymorphic
uncertain data on the deterministic modeling of multi-physical behavior of saturated soils. For this purpose, we have chosen a consolidation initial value problem as a benchmark in order to be able to test and compare both existing and self-developed methods.
A two-phase model (solid body and fluid, both materially incompressible and linearly elastic) was prepared within the framework of the Theory of Porous Media (TPM), so that the otherwise deterministic FEM calculations can be calculated automatically with probabilistic and stochastic approaches (in FEAP). Furthermore, we have developed a user-friendly tool (in R) for the generation of random fields with different properties. The tool allows to model aleatoric uncertainties, such as soil properties for several soil layers, and epistemic uncertainties, such as the numberof layers, their positions and geometries. For the practical realization between R and FEAP, a shell script has been created that controls the automated organization and processing of the individual batches of random fields and provides the outputs of the TPM in a suitable and organized format for the following analyses. By applying the Monte Carlo approach, we have analyzed the development of fluid pore pressure over time as well as the settlements due to own weight and varying top surface loads. Furthermore, the combined impact of a variation in correlation lengths and the natural variability of properties was investigated by a fuzzy-probabilistic approach.
Alongside these global uncertainty quantification approaches, another focus was on the development of the variational sensitivity analysis for the underlying physical model (TPM), which can be assigned to the local uncertainty quantification methods. The theoretical derivation of the model equations as well as the implementation in FEAP led to an efficient algorithm, which provides extensive information about the considered problem with only one deterministic calculation. For appropriate evaluation and assessment, different sensitivity measures have been developed, which provide information about the influence of individual parameters (global impact analysis) but also about the spatial distribution of a parameter (local impact analysis). The advantages and disadvantages of the different methods were worked out on the basis of comprehensive calculations and evaluations.
In parallel, the DEIM method was prepared for the TPM in order to reduce the computational effort for analyses that require a high number of model runs.
Essential project findings
- Variational sensitivity analysis of the theory of porous media for a two-phase model (solid body/fluid)
- Monte Carlo method for random fields
- Fuzzy-probabilistic investigations of polymorphic uncertainties
- Analysis of advantages and disadvantages of the different approaches
- Development of user-friendly tools for the application of uncertainty quantification methods
- Solution of interface problems between FEAP and R
- Implementation of reduction methods (especially DEIM) for the theory of porous media in order to accelerate model runs

Prof. Ricken
Prof. Dr.-Ing. Tim Ricken
Universität Stuttgart
Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen
Fakultät für Luft- und Raumfahrttechnik und Geodäsie

Prof. Ickstadt
Professor Dr. Katja Ickstadt
Technische Universität Dortmund
Fakultät Statistik
Lehrstuhl für mathematische Statistik und biometrische Anwendungen

Fr. Henning
Carla Henning, M.Sc.
Universität Stuttgart
Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen
Fakultät für Luft- und Raumfahrttechnik und Geodäsie
- Henning, C., Ricken, T.:
Polymorphic Uncertainty Quantification of Computational Soil and Earth Structure Simulations via the Variational Sensitivity Analysis,
(PAMM) 2019, Link - Pivovarov, D., Willner, K., Steinmann, P., Brumme, S., Müller, M., Srisupattarawanit, T., Reese, S.:
Challenges of order reduction techniques for problems involving polymorphic uncertainty, (GAMM -Mitteilungen) 42 (2) 2019, Link - Drieschner, M., Matthies, H. G., Hoang, T. V., Rosić, B. V., Ricken, T., Henning, C., Weinberg, K.:
Analysis of polymorphic data uncertainties in engineering applications,
(GAMM-Mitteilungen) 2019, Link - Schmidt, A., Henning, C., Herbrandt, S., Könke, C., Ickstadt, K., Ricken, T., Lahmer, T.: Numerical studies of earth structure assessment via the theory of porous media using fuzzy probability based random field material descriptions,
(GAMM-Mitteilungen) 42 (1) 2019, Link - Henning, C., Herbrandt, S., Ickstadt, K., Ricken, T.:
Combining Finite Elements and Random Fields to Quantify Uncertainty in a Multi‐phase Structural Analysis (PAMM) 18 (1) 2018, Link - Henning, C., Ricken, T.:
Polymorphic uncertainty quantification for stability analysis of fluid saturated soil and earth structures, (PAMM) 17 (1) 2017, pp 59-62 Link
