Dynamic analysis of prosthetic structures with polymorphic uncertainty
A continuation of the topic is currently taking place in the second project phase.
-
The main goal of this project is the design and development of a simulation framework focusing on the motion of the human lower extremity with different types of hip and knee prostheses in the presence of data as well as model uncertainty of aleatoric and epistemic character and to assess the uncertain results.
-
The project integrates modeling of the structures (human lower extremities and prostheses) and uncertainties, the mathematical formulation of the motion (as dynamical system or optimal control problem) as well as the computational methods (based on structure preserving integration) to solve the resulting differential algebraic equations.

Standing high and long jump movements
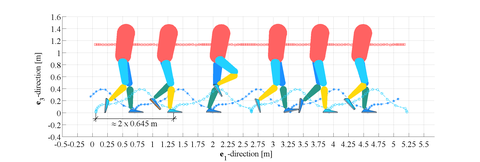
Three-dimensional gait simulation
Summary of the first funding phase
In the first phase, work in the subproject 14 of the priority programme SPP1886 is following two lines of research – a methodological one and a modelling one. Two first two published papers develop methodological aspects for the consideration of epistemic uncertainty in forward dynamics and optimal control simulation. The paper ’Fuzzy uncertainty in forward dynamics simulation’ presents a continuous formulation of fuzzy uncertainty forward dynamics and develops a corresponding temporally discrete formulation for forward dynamics simulation. The concept of multiple internal numerical differentiation (MIND) (extending the existing concept of internal numerical differentiation (IND)) yields the derivation of an approximate formulation of the corresponding α-level optimisation problem. This is included in our new Graph Follower algorithm (GF). The second fundamental work ’Epistemic uncertainty in optimal control simulation’ extends the first one to the simulation of optimal control problems. Here, the simulation method discrete mechanics and optimal control (DMOC) is used with possibly uncertain parameters like initial conditions, geometric quantities, material parameters or end conditions. Comparisons with benchmark solutions demonstrate that the developed methods show very good performance with regard to accuracy and efficiency for example systems with up to 22 uncertain parameters.
Furthermore, the fuzzy dynamics of a multibody system with polymorphic uncertainty in the material microstructure has been investigated jointly with subproject 18 of the SPP 1886 at the Chair of Applied Mechanics (LTM) at FAU resulting in another paper. Challenges of order reduction techniques for problems involving polymorphic uncertainty are considered in a joint publication with many other subprojects.
On the other hand, different models of a prosthetic foot have been established and used in simulation in three Master theses. The most complex one models the compliant behavior of the dynamic response prosthesis and is currently integrated in the project work. In particular, the model is based on a precurved stress-free initial configuration and allows to analyse the resulting internal stress with greater precision while requiring less computational effort than a three-dimensional finite element model.
Prof. Dr.-Ing. habil. Sigrid Leyendecker coordinated (jointly with Prof. Dr.-Ing. habil. Kai Willner, LTM) the journal publication on `Challenges of order reduction techniques for problems involving polymorphic uncertainty’ with contributions from twelve subprojects of the SPP 1886 and organised a Complex D workshop (jointly by LTM and LTD) at FAU during March 14-15, 2017, with 27 participants from twelve subprojects.
Essential project findings
-
development of a methodological framework for the consideration of fuzzy uncertainty in forward dynamic simulations
-
graph follower algorithm (GF)
-
multiple internal numerical differentiation (MIND)
-
approximate description of system outputs as a function of uncertain parameters
-
development of a methodological framework for the consideration of fuzzy uncertainty in optimal control simulations
-
simulation of two simplified gait cycle phases as optimal control problem
-
precurved stress-free geometrically exact beam model of carbon spring foot prosthesis
-
fuzzy dynamics of multibody systems with polymorphic uncertainty in the material microstructure

Prof. Leyendecker
Prof. Dr.-Ing. habil. Sigrid Leyendecker
Friedrich-Alexander-Universität Erlangen-Nürnberg
Lehrstuhl für Technische Dynamik

Eduard S. Scheiterer
M. Sc. Eduard S. Scheiterer
University of Erlangen-Nuremberg
Chair of Applied Dynamics
- Publication 1
