A hybrid Sampling-Stochastic-Finite-Element-Method for polymorphic, microstructural uncertainties in heterogeneous materials
A continuation of the topic is currently taking place in the second project phase.
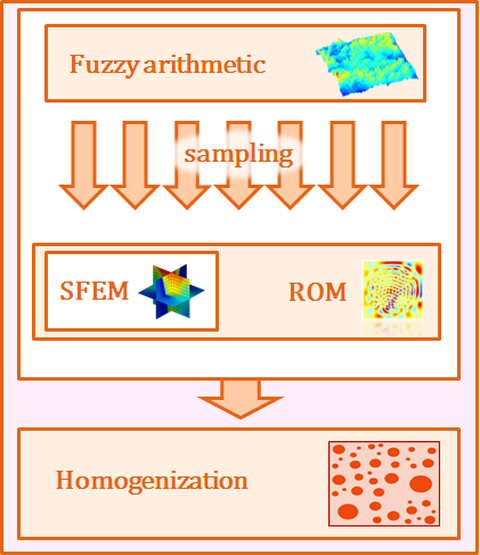
Project Flow: Establishing a combination of SFEM, ROM and Fuzzy Arithmetic and its application to Computational Homogenization problems.
The overarching goal of the proposed project at the methodological side is to establish a computationally tractable numerical method that is suited to capture polymorphic uncertainties in large-scale problems (as arising from the numerical analysis of heterogeneous materials microstructures). On the one hand the method will allow for fuzzy probability distributions of the random parameters (describing a microstructures geometry) and on the other hand the method will be based on only a few reduced basis modes. These ingredients will enable to capture epistemic uncertainties in addition to aleatoric uncertainties in a computationally accessible manner. The overarching goal of the proposed project at the application side is to establish a non-deterministic macroscopic material model. On the one hand the model accounts for the heterogeneity of the underlying material's microstructure by computational homogenization, and on the other hand it captures polymorphic uncertainties in the geometry description of the microstructure. The non-deterministic macroscopic material model then represents the necessary input for the mechanical design of macroscopic (engineering) structures under due consideration of polymorphic uncertainties in the heterogeneous materials microstructure.
Summary of the first funding phase
The effective macroscopic properties of heterogeneous materials result from the response of the underlying microstructure and can be estimated using either analytical or computational homogenization. Analytical homogenization approaches to determine the macroscopic behavior of heterogeneous materials are oftentimes restricted to linear problems. In contrast, computational homogenization can be applied to challenging, arbitrary linear and nonlinear problems.
Computational homogenization requires two separate Finite-Element models: a macroscopic model of the macrostructure (the structural engineering problem) and a microscopic model of the materials’ underlying microstructure. Thereby computational homogenization involves two main ingredients: transfer of the macroscopic loading to the microscale and averaging the corresponding response of the microstructure to obtain the effective macroscopic properties. The transfer of the macroscopic loading to the microscale can be performed, e.g., by applying either Neumann, periodic or Dirichlet boundary conditions (satisfying the Hill-Mandel condition) to the microstructure.
A technically challenging aspect for computational homogenization is the proper modelling of the material microstructure. It is even more challenging for materials with uncertainty in the microstructure, as considered in this project.
The aim of Phase I is the establishment of a fuzzy-stochastic FEM based framework for computational homogenization of heterogeneous materials in the presence of polymorphic uncertainty in the microstructure. In particular, the focus is on the efficient and accurate simulation of the uncertain microstructural response to be homogenized computationally.
In Phase I of the project we first designed a fuzzy-stochastic benchmark example for a microstructure of heterogeneous materials with uncertainly distributed inclusions. Based thereon we established the following novel techniques for stochastic and fuzzy-stochastic problems:
- Isoparametric stochastic local FEM,
- Isoparametric fuzzy local FEM,
- Fuzzy eXtended FEM,
- Isoparametric fuzzy-stochastic local FEM,
- Fuzzy-stochastic eXtended FEM,
We performed simulations using hybrid sampling-spectral fuzzy-stochastic FEM and fully spectral fuzzy-stochastic FEM. For the order reduction in the stochastic domain we introduced:
- The global Galerkin method with eXtended Fourier basis,
- The reduced model based on eigenvectors of a deterministic auxiliary problem,
- Incorporation of the POD into the stochastic local FEM,
- Element based discrete empirical approximation.
In order to accelerate the solution and to avoid expensive fuzzy sampling we furthermore introduced a method based on an equivalent model with reduced dimensions and applied this method instead of fuzzy sampling.
Essential project findings
- Development of an accurate stochastic FEM framework for aleatoric uncertainty
- Development of a hybrid fuzzy-stochastic FEM framework for polymorphic uncertainty
- Incorporation of reduced order modelling into the stochastic FEM
- Incorporation of reduced order modelling into the hybrid fuzzy-stochastic FEM
- Application to a benchmark example for materials with uncertain microstructure data

Hr. Pivovarov
Dmytro Pivovarov, M. Sc.
Friedrich-Alexander-Universität
Erlangen-Nürnberg
Lehrstuhl für Technische Mechanik (LTM)
- Publication 1


